本文是一篇工程硕士论文,本文首先阐述了我们所要研究的调度问题的现实背景及其研究意义,归纳和整理了近些年关于机器可用性约束、交货期、加工收益的国内外研究现状,总结了本文所研究问题的创新点。
第1章 绪论
1.1 背景及其意义
制造业是国民经济的主体,是实体经济的核心竞争要素,同时它也反映了一个国家的综合国力。2012 年,中国制造业占全球制造业比重为 22.5%,到 2020 年,这一比重提升到 30%。中国制造业正将中国推向全球供应链的核心位置,为中国经济乃至世界经济都做出了重要的贡献。然而,中国制造业在快速发展的同时,也面临诸多的挑战,例如创新能力不足、产品附加值低、产能过剩严重、高端人才匮乏、资源环境紧张、企业税负过重等问题。《中国制造 2025》指出当前全球制造产业格局正面临着重大的变化,中国必须要全面推进制造业转型升级,向高精尖产业方向发展,坚持创新驱动、质量为先、绿色发展、结构优化、人才为本的基本方针,推动中国从制造大国迈向制造强国。
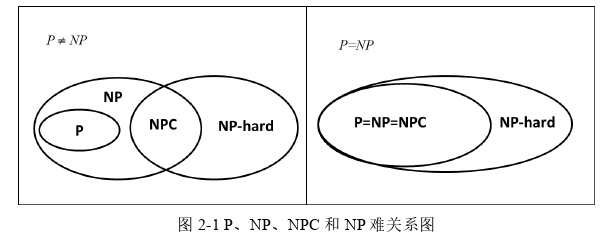
调度(Scheduling),也称排序,主要研究在满足一定约束条件下,通过合理的调度策略来分配有限的资源以获得最大的收益,比如最小化加工成本,最大化加工收益等等。调度的实质就是一个决策过程,要求决策出任务的合理安排以实现全局下的最优结果。随着我国制造业信息化、现代化程度的加强,调度在供应链制造领域备受关注。调度可以解决供应链中资源配置、信息滞后、供应能力、物流成本高等诸多问题。由于供应链中的每个角色面对的生产环境、生产资源、加工能力、企业战略、优化目标都是不相同的,因此企业需要根据自身的状况制定适合企业发展的调度策略,同时根据供应链的变化及时调整调度方案。
在经济全球化和信息技术快速发展的环境下,制造供应链之间面临着激烈的竞争。供应商在制造供应链当中扮演着非常重要的角色,优秀的供应商能够对下游企业起到领导的作用,整合制造资源,为下游的生产制造注入源源不断的动力。但同时,若供应商的供货能力出现问题,不仅给下游制造商造成较大的压力,还会导致下游供应链发生一系列连锁反应。
1.2 国内外研究现状
1.2.1 关于机器可用性约束的国内外研究现状
机器可用性约束,也称机器不可用时间段(machine unavailability period),即在一段时间内机器是不可以加工任何工件。如果某个工件在加工过程中恰好遇到机器维护而被中断,那么这个工件只能在之后重新开始加工。以前大多数研究文献都假设机器在整个计划范围内都可以连续使用,但是该假设却偏离实际的工业设置。直到 Lee(1996)首次在论文中阐述了一个机器具有可用性约束的单机调度模型。他认为,在绝大多数现实生产场景中,机器并不是始终可用的,必定受到一些限制使得机器在一段时间内无法运转,这些限制包括机器突发故障、定期维护、工件人员休息等等。Lee提出的模型很快受到了学者们的关注,在此后 20 多年里,许多扩展成果也是基于 Lee的基本模型而建立的。Lee(1996)在基本模型上,按照工件在被中断后是否可以继续加工,将工件加工方式又分为可恢复和不可恢复。Braun 等(2002)加工一个给定机器不可用时间段的调度问题,最小化两台机器的最大制造期。Brauner 等(2009)首次将操作不可用时间段引入调度问题,给出明确的概念和应用场景。Xu, Yin 和 Li(2009)考虑在柔性维修活动下的不可恢复单机调度问题,目标是极小化最大制造期。Mosheiov 和 Sarig(2009)研究具有一个速率调整的维修活动的单机时间窗调度模型。之后,Mosheiov 和 Sarig(2009)又将单机模型扩展到平行机调度问题上。Tan 等(2011)考虑一个平行机调度模型,目标为最小化最大完工时间,其中维修活动仅在给定的机器集上执行。Hasan 等(2011)研究具有不可用时间段的作业车间调度问题。Rustogi 和 Strusevich(2014)引进一个更一般的维修调度模型,目标是最小化最大制造期和总的完工时间,其中工件的加工时间是依赖于工件加工的位置和时间效应的一个组合函数。Hashemian 等(2014)考虑了具有多个计划不可用时间段的可恢复作业的并行机调度问题,以最大程度地缩短了工期。
第2章 基本理论介绍
2.1 组合优化问题概述
组合优化(Combinatorial Optimization)通常也被称作离散优化,是一类最优化问题,也是运筹学中的一个非常重要的研究分支。组合优化问题是一类在离散状态下求极值的问题。许多现实生活中的案例通常可以被抽象概括成离散优化问题,离散优化问题在一些重要场景和领域例如系统工程、信息技术、生产管理等都十分常见。典型的组合优化问题有旅行商问题(Traveling Salesman Problem-TSP)、生产调度问题(Production Scheduling Problem) 、 0-1 背包( Knapsack Problem )问题、装箱( Bin Packing Problem)问题、图着色问题(Graph Coloring Problem)、聚类问题(Clustering Problem)、指派问题(Assignment Problem)、集合的覆盖(Set Covering Problem)问题、设施选址(Facility Location Problem)问题、网络流(Network Flow Problem)问题、可满足性(Satisfiability Problem)问题等。本文研究的是组合优化问题中的生产调度问题。
2.2 算法
2.2.1 概述及算法应用
随着新兴技术的快速发展,无人驾驶、人脸识别、人工智能、图像加工、物联网等技术运用越来越广泛,而支持这些新兴技术发展的算法起到了关键性的作用。算法可以被看作是对一类解决方案准确和完整的描述,是解决一系列问题的精准指令。算法中的指令可以认为是事先定义好的计算过程,该过程取某个值或值的集合作为输入以此产生某个值或值的集合作为输出,这样算法就是把输入转化为输出的计算步骤的一个序列。通常一个算法具有五个特征:输入项,输出项,有穷项,确定性和可行性。输入项是指在运行算法前需要输出初始参数或者定义相关初始条件;输出项是指在算法运行结束后输出结果;算法的有穷性是指一个算法的描述应该由有限多条指令或语句构成,换言之算法必须要用有限长的语言来描述;确定性是指作用于所求解问题的给定输入,根据算法的描述将产生出唯一的确定的一个动作序列;可行性是指算法中指令或语句的含义应该严格且明确,所描述的操作过程可以完全机械地进行。在生产调度问题中,目前主要存在用以下几类算法求解。
启发式算法通常是一个基于直观或者经验构造得到的算法,在付出一定的代价(计算时间、占用空间等)下给出待解决组合优化问题每一个算例的可行解,但该可行解与最优解的偏离程度往往是无法预估的。在许多实际问题当中,要得到最优解往往需要花费指数级的时间,这对任何人都是无法忍受的,退而求其次,可以通过启发式算法在较短的时间内求得问题的一个可行解,解的质量与指数时间有关。常用的启发式算法 包 含 贪 心 算 法(Greedy Algorithm)、 局 部 搜 索(Local Search)、 遗 传 算 法(Genetic Algorithm)、模拟退火算法(Simulated Annealing)等。
第 3 章 基于公共交货时间窗和机器可用性约束的单机调度模型 ......................... 21
3.1 本章研究内容 ........................... 21
3.2 符号说明 ........................................... 21
3.3 问题描述 .............................................. 22
第 4 章 基于交货期与机器可用性约束的单机调度模型 ......................................... 38
4.1 本章研究内容 ....................................... 38
4.2 符号说明 ........................................... 38
4.3 问题描述 ..................................... 38
第 5 章 基于公共交货期与机器可用性约束的平行机调度模型 ............................. 45
5.1 本章研究内容 ............................. 45
5.2 符号说明............................45
第6章 算例分析
6.1 动态规划 DPA 算例分析
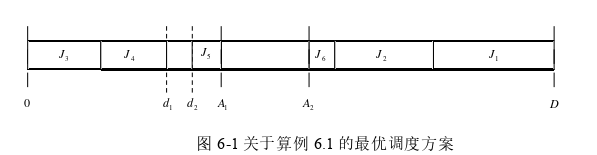
本章将分别对前三章提出的动态规划与近似算法进行数值实验并对其算法运行得到的数值结果进行分析。对于动态规划算法,我们首先任给一个小规模算例,使用Python 编写动态规划算法并求解,得到算法解,然后通过枚举的方式得到最优解,将算法解与最优解进行比较,验证其动态规划算法的正确性。接着,我们会调整问题的规模(工件数),在给定范围内随机选择工件参数(工件加工时间 、交货期 、机器不可用时间段 ),随着问题规模的增大,通过测试动态规划的平均运行时间来评估其算法的性能。
第7章 总结与展望
7.1 研究工作总结
本文从制造供应链背景出发,结合当前生产调度理论研究热点,提出了三个基于交货与机器可用性约束的机器调度问题。近三十年以来,研究交货期或者机器可用性约束的学者有很多,他们提出了很多基于此工件特征的调度模型,但是研究将两者约束相结合的调度模型的学者却很少。为此本文为解决现实生产制造问题以及弥补研究空白,提出了相应的调度模型。具体的研究内容如下:
(1)首先阐述了我们所要研究的调度问题的现实背景及其研究意义,归纳和整理了近些年关于机器可用性约束、交货期、加工收益的国内外研究现状,总结了本文所研究问题的创新点。
(2)介绍了本文研究问题所涉及到的基本调度理论。首先阐述了组合优化问题的基本知识,然后解释了算法的基本概念以及解决组合优化问题常用的算法,并对调度问题的计算复杂度理论进行了说明。接着,介绍了生产调度问题的定义以及符号解释,并对本文研究问题所需要使用的算法以及 Python 进行了着重介绍。
(3)第 4 章提出了基于交货期与机器可用性约束的单机调度模型,目标是极大化加工收益。极大化加工收益是近几年提出一个比较新颖的优化目标,但是在现实却有很多应用场景。在制造供应链当中,当无法避免工件出现延迟交付的情况时,供应商和制造商都希望能够加工尽可能多的工件,使得自身的生产效益最大化。因此供应商在生产过程中,出现加工收益较低的情况,就需要及时调整调度方案,减少制造资源的浪费。本章提出的问题是一个 NP 难问题,之后我们证明了此问题的一些最优性质,并且利用这些性质设计了动态规划算法 DPB,该算法的时间复杂度为 。
参考文献(略)
