本文是一篇计算机论文,本论文对模糊环境下的多目标优化问题进行了探索和研究,并取得了一定的研究成果。但是由于科学技术的发展和社会的进步,仍有许多问题值得去继续研究和探讨。
第 1 章 引言
1.1 研究背景及意义
1.1.1 研究背景
多目标优化已经被应用到多个重要的领域,例如:金融投资[1]、信用风险评估等[2]。寻找在特定条件下同时满足多个目标的最优解是多目标优化的主要目标。然而,在实际情况中,人们很难用数值型数据正确描述优化问题中的各项变量,因此,最优决策不易得出。大多数繁琐复杂问题中都存在模糊不确定性的数据信息,它们存在于各个领域中,如自然科学研究、医疗保健、经济生活、社会民生等。对当前世界中可能存在的各种不确定性和变化现象进行数学分析和处理,是当前社会发展过程中的现实课题。研究人员经常使用模糊集理论、可能性理论和概率论等几种主要的数学方法和工具来处理这些存在不确定性的现象。不确定性规划理论就是不确定性环境下的系统优化理论研究的重点。随机性规划和模糊性规划是经典的不确定性规划的两大类[3-5]。多目标规划和模糊数结合的相关方法已经应用到多方面。Su 等[6]建立了带有变量的模糊多目标线性规划模型,将模型参数用模糊数表示,区间值是利用隶属度函数转变的。Liu 等[7]提出模糊随机多目标规划问题,并构建了混杂智能算法进行求解。
模糊集理论属于三种不确定性理论之一,其内在具有某种不确定性。模糊集理论是对现代化经典 Cantor 集理论的有益拓展,将一个经典的二值逻辑理论拓展延伸为一个连续的区间逻辑,更好地解决了许多现实中的模糊问题。模糊决策的方法主要是以模糊数学作为理论依据进行精确和量化决策,具有以下基本特点:(1)完成全部或者局部的决策信息都具有模糊性;(2)在模糊集理论的基础上研究量化决策方法;(3)最终决策结果含有一定的模糊性,但是经过转变可以称为确定的结果;(4)模糊决策也同样应该具备普通决策的一般性[8]。最常见的模糊数是区间型模糊数和 L-R 型的模糊数,比如:三角形的模糊量和梯形的模糊量。
1.2 国内外研究现状
在分类方法中,数学规划的方法是一类重要的并在实际应用中使用较多的非统计的方法。其中,线性规划最大的优点就是它可以把一个决策者的偏好当作是一种有限度的约束性条件添加到模型,并且能够得到线性的、易于解释和部署的模型。但是,实际应用中的数据结构并非总是线性的。因此,基于核的线性规划的方法、非线性规划的方法和其他数学规划的方法将是一个重要的发展方向。
对于最优化线性规划模型来说,Mangasarian 等[13]首次认识到可以把线性规划的最优化方法运用到分类问题中;直到 Freed 等[14]研究得出了比较简单的两分类模型,即使得错误分类的样本点到分类边界的偏差之和最小或者正确分类的样本点到分类边界的距离之和最大;在基于上述两种度量的混合模型[15,16]提出后,才逐渐引起了更多学者的兴趣和重视。Joachimsthaler 等[17]将这一领域内的重要的文献进行了概括和描述。一部分学者对基于统计的分类方法与线性规划方法的效果进行了比较分析,尽管 Nath 等[18]研究认为统计的方法要比线性规划的方法好,但绝大多数的研究者则持相反意见。Bennett 等[19]研究了将线性和二次最优化问题应用到模式识别问题中进行了很有价值的讨论。在此基础上,Mangasarian 等[20]将这些观点进行了进一步的拓展,并设计了较大数据集上的数据挖据算法。Glen等[21,22]研究了利用整数规划来解决分类问题的方法,即使错误分类的样本数目达到最小。Shi 等[23]研究发现在使用多目标线性决策的方法进行数据挖掘建模时,同时考虑尽可能最小化两类之间总体的重叠程度和最大化两类数据到各自边界的距离,将会极大地提高模型的计算能力,可以求解并得到不同分类问题的妥协解。Kou 等[24]提出了用于解决多分类问题的多类多目标规划模型。Peng 等[25]在多目标线性规划和支持向量机分类的基础上提出了多目标凸二次规划的分类模型,以解决多目标线性规划算法在速度和可扩展性方面存在的问题,并将该方法应用于信用评分和网络入侵检测等方面。Shi[26]针对多目标线性规划分类模型存在的解不稳定的缺陷,提出了正则化的多目标线性规划分类模型,即通过在模型中引入正则项来改进模型的求解性能。
第 2 章 相关理论基础
2.1 数据标准化
数据标准化是把样本的特征值缩放到一个特定的范围内。数据标准化产生的原因:某些算法规定要求样本具有零均值和单位方差;需要消除样本不同特征具有不同数量级的影响[32]。为了消除与数据特征之间测量纲相关的影响,需要通过数据标准化的处理,来解决与数据特征之间的相互可比。原始数据在经过数据标准化的分析处理后,各个特征都是在同一数量级,适宜于进行整体综合的对比和分析。
李登峰等[36]在深入分析,系统研究了多人对策的基本问题以及运行规律的理论基础上,将多人对策、多目标决策和模糊集理论相互交叉结合,提出并积极探索关于建立新的模糊多目标多人决策基本理论和实践模型。高新波等[37]参与研究了模糊聚类分析技术,他较为系统地探讨了基于目标函数模糊聚类的基本理论和方法等;Shi 等[38]研究并总结了多目标规划模型的分类、多阶段多目标模糊线性规划分类的一类模糊计算处理方法和分析模型,并将其应用在信用评分等商业领域。
模糊集(Fuzzy set)通常是一种用来处理模糊的各种不确定性数据信息的有力计算工具,而人们在进行战略决策时常常遇到模糊的处理不确定性信息现象,因此,使用模糊集理论来解决实际问题已经成为学术界和工业界一个共识和行之有效的方法之一。对于如何处理含有模糊参数的最优化问题,模糊数学规划提供了更好的解决方法。但是,对于含有模糊参数的数学规划和多目标规划方法在数据挖掘和知识发现中的应用研究的还不多并且不够深入,还有许多值得探讨的地方。
2.2 模糊隶属度
模糊集理论的根本思路在于模糊或灵活化经典集合中的绝对隶属关系,并在此基础上形成了关于模糊集的计算、语言变量表示、近似推理等理论体系。随后,在多目标决策的基础上,Bellman 等[33]人提出把决策者无法准确定义的参数、概念、条件等转化成合适的模糊集,以改进决策的准确性和效率。这是模糊决策的一个基本模型。随后,模糊集理论和方法开始渗透到科学研究的各个领域。Zimmermann等[34]将其引入线性规划问题,至此,模糊线性规划问题被广泛研究。后来 Joseph等[35]人将模糊逻辑用于数据挖掘方法中,并深入探讨了模糊专家系统、基于模糊集的关联规则算法以及基于模糊逻辑的软回归等方法。
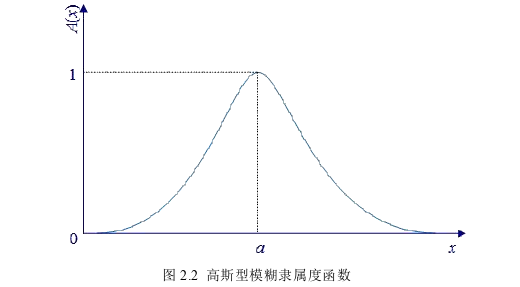
本章将在描述模糊集基本理论、模糊决策理论和模糊数学规划的基础上,探讨和分析模糊多目标规划分类的各种模型和算法,以便改进多目标规划分类方法的效率、提高模型的分类准确率和模型在新数据集上的推广能力。下面将简要介绍常用的模糊隶属函数。
第 3 章 基于均值模糊多目标线性优化的软件缺陷预测.......................18
3.1 软件缺陷检测...........................18
3.2 模型构建...................................19
第 4 章 基于模糊多目标二次优化的信用评分模型研究................................29
4.1 基于近似三角模糊数的多目标二次优化分类器模型...........................29
4.1.1 近似三角模糊隶属函数.............................................29
4.1.2 近似三角模糊特征核矩阵............................................30
第 5 章 面向类不平衡的模糊多目标二次优化模型研究及应用.........................................38
5.1 改进的模糊多目标二次优化分类器模型...................................38
5.1.1 近似高斯模糊隶属函数.......................................38
5.1.2 近似高斯模糊特征核矩阵.......................................39
第5章 面向类不平衡的模糊多目标二次优化模型研究及应用
5.1 改进的模糊多目标二次优化分类器模型
本节主要详细阐述 AGF-MOQOC-FS 分类器的构造。首先定义近似高斯模糊隶属度函数的计算公式,并将其与核函数结合,构造近似高斯模糊核矩阵。然后,将该矩阵与类不平衡惩罚因子推广至 4.2 节的 ATF-MOQOC-FS 中,构造面向类不平衡数据集的 AGF-MOQOC-FS 模型。
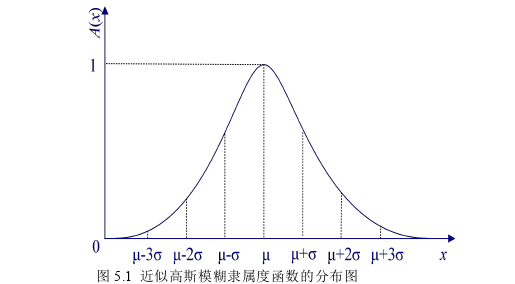
5.1.1 近似高斯模糊隶属函数
第 6 章 总结与展望
6.1 本文工作
本文分别利用均值模糊数、近似三角模糊数、近似高斯模糊数描述不确定系统中的不确定性信息,研究模糊多目标规划模型及其算法,并且探讨多目标规划在软件缺陷预测及信用评分中的应用。本文的主要工作与成果具体如下:
( 1 ) 在分类问题中,大多数数据集是非线性可分的。选择合适的核函数将数据从输入空间映射到高维特征空间,让非线性可分问题转化为线性可分或近似线性可分的问题进行求解。此外,数据中存在一些噪声、孤立点和异常值等数据,多目标线性规划分类器对此类数据非常敏感,会导致错误分类。因此,提出相应的模糊隶属度函数,应对数据集中的特异点。最后,在多目标线性规划模型的中引入了稀疏因子,约简特征数去除数据集的冗余特征。
( 2 ) 在标准的三角模糊隶属度函数的基础上,利用 3原则,进行了改进,使其引入多目标二次优化模型之后,提高模型的分类准确率,且在实际应用中能有更好的泛化能力。
(3)提出了面向类不平衡数据集的带有特征选择的近似高斯模糊多目标二次优化分类器(Multi-objective quadratic optimizing classifier based on approximatelygaussian fuzzy number with feature selection,AGF-MOQOC-FS)。在(2)的研究基础上,为了解决数据集类别不平衡的情形下,模型对多数样本类别过拟合的现象,以及分类精度降低的问题,本文基于代价敏感的学习方法,在(2)的模型中引入类不平衡惩罚因子,以解决上述问题。此外,模型中还引入了新构造的近似高斯模糊隶属度函数,虽然它计算复杂,但是能更好的拟合数据集,在实际分类数据应用中表现出更好的泛化能力,提高了分类器的鲁棒性。最后,本文将(1)、(2)和(3)中提出的三类模型都应用在信用评分数据集中,经过实验分析发现,面向类不平衡数据集的 AGF-MOQOC-FS 模型具有更好的分类性能。
参考文献(略)
