本文是一篇金融论文代写,本文使用傅里叶变换方法能有效提高模型参数的估计速度,有效解决模型中存在的“时间负担”问题,提高了波动率风险溢价的估计效率。
第 1 章 绪论
1.1 研究背景与问题提出
1.1.1 研究背景
1.1.1.1 实践背景
(1)金融市场的新时代
为健全我国资本市场体系,优化资源配置,2014年 5 月 8 日,国务院印发了《关于进一步促进资本市场健康发展的若干意见》,提出要逐步丰富我国金融衍生品市场,推出股票、股指及商品等期权,同时,又为了有序规范我国期权试点业务,进一步加强风险管理,防范市场出现系统性风险及保护投资者的相关权利,推进期权市场健康稳定有序发展,证监会与 2014 年 11 月25 日审议通过了《股票期权试点管理办法》。接着,上海证券交易所发布了《上海证券交易所股票期权试点交易规则》。2015 年 2 月 9 日,经证监会批准,上海证券交易所正式上市交易上证 50ETF 期权,标志着我国 A 股市场场内股票期权“零”的突破。2019 年 11 月 8 日,深圳证券交易所发布关于就《深圳证券交易所股票期权试点交易规则(征求意见稿)》公开征求意见的通知,将平稳有序推进沪深 300ETF期权上市工作。深圳证券交易所开始股票期权的试点,这是金融市场支持粤港澳大湾区建设及深圳建设中国特色社会主义先行示范区的重要举措,将推进深市和沪市协调稳定发展,引导资金有序入市,增强金融市场稳定性,提高资金服务实体经济能力,使得我国金融市场进一步与国际市场接轨。这一系列举措,标志着我国金融市场正式进入“期权新时代”,同时也步入了一个期货期权等多产品化投资及市场风险管理的新时代。
(2)期权产品日趋丰富 我国目前推出的场内期权品种及数量相对较少,大致可以分为商品期权和股票期权两大类。2015 年 2 月 9 日,我国 A 股市场首支股票期权上证 50ETF 期权正式推出。2019 年 12 月 23 日,上海证券交易所和深圳证券交易所上市交易沪深 300ETF 期权合约,中国金融期货交易所上市沪深 300 股指期权合约。2017 年大连商品交易所及郑州商品交易所上市交易了豆粕、白糖期权,我国平稳有序地开启了商品期权时代。2018 年 9 月,上期所正式上市我国首个工业品商品期权-铜期权。根据上海期货交易所的发展规划,在商品期权上,原油、锌、铝等商品期权品种也将陆续上市。可以预期未来更多数量及种类的期权将在我国主要证券交易所陆续推出,比如个股期权、期货期权及波动率期权等,这将极大地丰富我国金融市场。投资者可利用期权产品构建各种投资策略,进而提升我国金融市场的运行及资源配置效率,也为进一步提升金融服务实体经济提供强有力的支撑。股指期权相较于商品期权交易量更活跃、受众更广泛、也更具代表性,上证 50ETF 期权在我国金融市场中发挥着极其重要的作用。目前,我国尽管已推出沪深 300 股指期权,但上市时间较短,而上证 50 指数在很大程度上也反应了我国股市大盘股的行情走势,因此,本文主要以上证 50ETF 期权市场为研究对象。
1.2 研究目的及意义
1.2.1 研究目的
期权是金融市场发展到一定阶段的必然产物,也是市场成熟的重要标志。美国成熟的金融市场的交易机制比较健全、产品比较丰富,而且机构投资者占比较大;然而,我国作为全球第二大市场经济体、最大的新兴社会主义市场经济体,期权交易在我国才刚刚起步。又由于我国独特的金融市场结构,有着不同于欧美等发达经济体的市场特点。因此,认识我国期权市场的定价情况和潜在风险特征,对我国金融市场的健康可持续发展就显得尤为必要。
本文旨在研究上证 50ETF 期权市场波动率风险溢价,具体研究目的包括以下几个方面:
(1)检验期权市场的定价效率 早期的 Black-Scholes 期权定价模型将波动率看作固定值,但实际上波动率是时变的(瞿慧等(2019)[1]),而且在实际市场中也常存在资产跳跃现象,跳跃也会被市场定价。因此,传统的 Black-Scholes 期权定价模型会出现定价效率不佳的问题,而本文采用随机波动率模型从已实现测度和风险中性测度研究的上证 50ETF 期权市场,既考虑波动率的随机性又考虑资产价格及波动的跳跃性,选取拟合市场最优的模型,使得上证 50ETF 期权定价更有效率。
(2)构建波动率风险溢价的测度方法 面对金融市场的“异象”,国外学者纷纷对波动率风险溢价展开研究。虽然对波动率风险溢价的估计存在分歧,但随着研究的深入,在波动率风险溢价的测度上也有逐渐趋同的迹象;本文借鉴国内外已有的研究成果,从已实现测度和风险中性构建波动率风险溢价的测度方法,解释金融市场“异象”。
(3)揭示波动率风险溢价之谜 国内外学者在进行波动率风险溢价相关研究时,由于所研究的市场以发达金融市场为主,采用的样本频率及研究方法有所不同,因此,得出的结论也不尽相同,部分研究甚至出现了相反的结论,并未对波动率风险溢价之谜进行详细的阐述。本文综合国内外已有研究成果,将从传统的金融学定价理论出发,探索期权定价、投资者行为及波动率风险溢价三者之间的内在联系,揭示金融市场中的波动率溢价之谜。
第 2 章 波动率风险溢价的理论研究
2.1 波动率风险溢价的理论依据与思考
2.1.1 传统金融学理论与思考
2.1.1.1 资产定价理论及思考
(1)资产定价理论
一直以来资本资产定价理论都是金融学领域最重要的主题之一,学者们对其进行了大量研究(Markowitz(1952)[60]、张维(2012)[61])。其主要用来解释在市场不确定性条件下支付未来证券的价格或者说价值,其中证券的价格是由市场供给和需求共同决定的,同时也是市场均衡时的价格;在确定性的理想化的世界里,资产定价过程较为简单,用无风险利率或者确定性的回报率通过一定的方法折现未来收益就可得到资产的价格;但是在实际的金融市场中充满大量的不确定因素,比如在不同时期投资者的风险态度也会有所不同,也给资产定价理论提出了挑战,市场中具有各种风险,给市场带来各种不稳定性,这里所说的风险是指资产价格在未来的走势与确定性价格之间的偏差。为了便于资产定价,人们也将资产定价公式简单化,比如资本资产定价模型(Capital Asset Pricing Model,CAPM 模型),即为在理想化的世界中的资产价格加上溢价因子,即资产价格大致等于无风险利率折现未来收益,再叠加一个风险溢价因子。面对不确定的市场,人们在进行资产定价时必须要考虑投资者在金融市场中风险与收益之间的权衡问题,投资者承担市场风险必须要获取额外的风险收益,而理论上仅考虑系统性市场收益风险,这样单一的考虑远远不能适应复杂多变的资本市场;多年来研究者也纷纷寻找新的风险源及风险溢价,希望拓展传统资产定价理论以便更好地认识市场(陈蓉等(2011)[25])。
(2)风险溢价
风险溢价是投资者在面对不同风险资产且明白高风险高收益、低风险低收益的情况下,判断其愿意承担风险获取相对较高的报酬或者不愿意承担风险仅接受确定收益,已确定收益与冒风险获得的收益之差就是风险溢价,风险溢价是投资者承受风险而获得的风险补偿。期权具有高杠杆、高收益,当然也伴随着高风险,近些年来随着期权等金融衍生品的发展,人们对风险源的研究更为深入,不再满足于股权风险溢价等一阶矩风险溢价,开始关注波动率风险溢价、相关性风险溢价、偏度及峰度风险溢价等高阶矩风险溢价(Yang 等(2018)[62]),而波动率风险是高阶矩风险的代表之一,波动率风险溢价之谜也是目前金融研究的热点(如:Chen 等(2016)[5]、Della 等(2016)[6]、Johnson 等(2017)[7]、Londono等(2017)[8])。
2.2 波动率风险溢价的数理模型及优化
2.2.1 随机波动率模型
金融市场微观结构理论是现代金融学领域中一个新兴且重要的分支,与其它金融学分支呈现相辅相成、相互交融的特点。市场微观结构有广义和狭义之分,按照 O'hara(1995)[81]的观点,狭义的市场微观结构是指证券交易价格的发现、形成过程和运作机。按照杨之曙(2000)[82]的研究观点,金融微观结构涉及的面较广,几乎涉及到了金融市场的各个组成部分,比如:交易技术规则、市场信息、市场参与者及各类金融工具等等。金融市场微观结构理论是在既定市场微观结构下,研究证券交易的过程及结果,包括证券的交易机制、投资者的行为、市场中的流动性、稳定性、交易成本、透明度以及有效性等等。
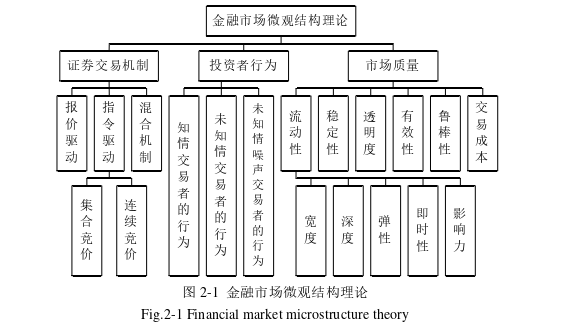
Cox 和 Ross(1976)[84]开创了的基于无套利的风险中性定价方法,风险中性假设是资产定价中的一个重要的思想,是一个理想化的世界,在风险中性世界里投资者对待风险资产和无风险资产的偏好也是相同的,在风险中性测度下资产的预期收益等于无风险收益。为了便于期权定价,这一思想后来广泛应用于期权定价中,所以在以后的 Black-Scholes 期权定价的推导过程中都接受了这样的前提假设条件。从已实现测度及风险中性测度两个维度,可以得到市场蕴含的风险溢价及投资者态度。
第 3 章 随机波动率模型的参数估计及市场特征分析 ....................... 39
3.1 引言 ....................................... 39
3.2 数据选择与预处理 .............................. 39
第 4 章 波动率风险溢价的信息特征分析 .......................................... 59
4.1 引言 .......................................... 59
4.2 波动率风险溢价的测度 ...................................... 59
第 5 章 波动率风险溢价与股票收益关系分析 ............................ 76
5.1 引言 ............................................ 76
5.2 波动率风险溢价与市场收益率相关性分析 ........................... 76
第 6 章 波动率风险溢价的影响因素分析
6.1市场微观结构变量对波动率风险溢价的影响
市场微观结构主要研究内容包括证券交易制度、投资者以及市场质量三个部分的内容(刘海龙(2003)[134])。国内外学者在研究波动率风险溢价影响因素时,考虑较多的是市场质量对波动率风险溢价的影响,如:市场波动性、市场深度、市场流动性等。主要原因有两点:一是,期权交易制度难以量化,没有统一的标准;二是,上证 50ETF 期权交易时间不长,期权市场的交易制度变化较少。在第四章,本文已近深入讨论了投资者行为与波动率风险溢价之间的关系,因此本节主要从讨论市场质量方面对波动率风险溢价的影响,又因为市场质量的衡量指标主要由收益率、波动率、交易量、市场流动性(换手率)、持仓量及买卖价差等金融市场微观结构变量组成,因此本节主要研究这些变量对波动率风险溢价的影响。
6.1.1研究假设
本文将选取市场微观结构变量中的市场活跃度、市场收益率、市场流动性及波动率、市场深度、交易成本等六大指标分析其对波动率风险溢价的影响。
(1)市场流动性
市场流动性是金融市场的生命之源,也是全球金融体系平稳的前提,流动性的剧烈变化往往是构成证券价格波动和金融不稳定的内在原因,当流动性发生枯竭时,往往会引发证券价格的剧烈波动,比如 2015 年中国金融市场“股灾”时发生的熔断事件,市场流动性问题也是一个重要原因。石广平(2020)[135]研究表明市场流动性对证券定价具有重要的影响;黄峰和杨朝军(2007)[136]等学者的研究也表明,流动性风险可被显著定价。苏冬蔚等(2004)[137]研究表明换手率可作为市场流动性的代表,市场换手率越高,市场流动性越大,换手率代表市场交易的活跃程度。郑振龙(2017)[56]认为换手率高意味着市场暴跌等极端风险出现的可能性增大,研究表明换手率与波动率风险溢价显著负相关。市场流动性风险被市场定价,对标的市场价格及期权价格均会产生影响,进而对波动率风险溢价也会产生影响。本文选取换手率作为市场流动性指标,假设:
H1:市场流动性越高与波动率风险溢价负相关,即换手率越高,波动率风险溢价越低。

结论
我国期权市场相较于欧美发达金融市场仍处于起步阶段,期权功能得到初步发挥,但是发展尚不成熟,同时也伴随着新的风险源及溢价,金融市场中的风险管理面临挑战,准确认识期权市场中的风险源对金融市场监管者、投资者及金融中介机构是至关重要的。本文以我国新推出的上证 50ETF 期权为研究对象,运用上证50ETF 及其期权市场日频交易数据,采用随机波动率模型及 MCMC、傅里叶变换法等方法,从已实现测度和风险中性测度中提取波动率风险溢价,本文的主要结论和创新点如下:
(1)建立了波动率风险溢价研究的分析框架,揭示了波动率风险溢价的形成机理。首先,基于资产定价理论及风险溢价、期权定价理论和行为金融学理论等阐述了波动率风险溢价的理论依据。其次,阐述了随机波动率模型期权定价相关的数理模型及优化方法,为全文提供理论及数理建模的支撑,为全文的研究奠定数理基础。最后,基于波动率风险溢价之谜,从期权定价及投资者行为两大视角揭示了波动率风险溢价的形成机理。本文的研究有利于补充期权定价理论及行为金融学理论。
(2)从期权定价视角出发,分析了模型的拟合优度及市场特征。一是,在已实现测度下根据 DIC 准则,DICSV>DICSVJ>DICSVCJ,即 SVCJ 的 DIC 值最小,SVCJ模型相较于 SV 模型和 SVJ 模型在现货市场具有更好的拟合优度。二是,在风险中性测度下,SVCJ 模型相较于 BS 模型、SV 模型和 SVJ 模型在期权市场具有更高的定价精度。三是,市场中存在跳跃非对称性、跳跃聚集和跳跃逆转等现象,当市场波动率较大时,资产收益及波动发生跳跃的概率及幅度较大,传统的 BS 模型、SV 模型难以捕捉市场中所发生的跳跃,而 SVCJ 模型能够捕捉资产收益及波动的跳跃现象。四是,由于跳扩散随机波动率模型复杂、涉及的期权交易合约众多,因此,计算时间冗长,本文使用傅里叶变换方法能有效提高模型参数的估计速度,有效解决模型中存在的“时间负担”问题,提高了波动率风险溢价的估计效率。
参考文献(略)
