本文是一篇金融论文,本文通过对我国资本市场波动率与尾部风险的研究,基于市场有效性理论,认为随着资本市场的完善和信息技术的发展,信息在资本市场中的传递效率增强,在当前背景下,使用传统的历史数据,特别是历史低频数据,对风险预测和风险控制很难起到较好的效果。考虑到期权市场的价格数据,不仅包含对于历史情况的评估也包含了市场参与者对于未来的预期,且我国期权市场以专业的机构投资者为主,对于市场的判断相对更加准确。
第 1 章 绪论
1.1 研究背景与意义
1.1.1 研究背景
资本市场是经济的重要组成部分,是实现长期经济社会发展和资源优化配置的重要途径。资本市场的核心作用是价格发现和风险控制,它可以为微观经济实体提供稳定的风险规避工具,稳定其生产运营。资本市场在发挥价格发现和风险控制作用的同时,需要市场上有大量的对冲交易者和投机者。在市场正常运行过程中,如果微观经济主体能够根据经济形势采取合理的交易行为,市场的整体运行将保持正常,但如果市场条件发生变化,不稳定因素增加,市场参与者的非理性行为等会导致市场产生剧烈波动,引发市场风险。近年来,随着资本市场的发展,不同的金融机构之间和不同地区之间的关联性进一步增强,一旦系统性风险爆发,所造成的危害程度会越来越大,风险传递的范围越来越广,这会给实体经济造成严重的影响。同时,科技的进步使得信息的传递速度加快,新的金融衍生品不断被创造,信息技术使交易方式的改变等,这些都改变了资本市场的传统规律,尽管金融衍生工具和新的交易方式有可以提高资本市场效率,降低成本等优点,但衍生工具的构造复杂性,价格变化不规律等特征也会放大市场风险,给风险管理者造成一定困难。资本市场是一个多层次,多目标的复杂系统,而且其复杂性呈指数级增长,跨市场和跨区域的传染性使得对资本市场体系的风险管理更加困难。
在我国实行供给侧改革,经济结构转型的背景下,资产价格的波动导致资本市场存在潜在的不稳定性,如果资本市场发生系统性风险,则会对实体经济造成严重冲击。我国金融工作会议反复强调要完善资本市场金融监督体系,防范发生系统性的金融风险,将工作重点放在关键领域的预防和缓解风险上。近年来,我国的经济结构和市场环境发生了很大变化,2001 年中国加入世界贸易组织,中国资本市场开放不断深化,大量境外资本得以快速且自由地流动,增强了中国资本市场的市场化程度,提高了市场效率,虽然市场规模日益扩大,但与之而来的金融风险以多种方式继续积累,当风险积累到一定程度,随之而来的可能是范围广,幅度大的市场风险,这种风险往往伴随着市场极端波动与市场风险事件。
1.2 文献综述
1.2.1 资本市场风险测度与方法
资本市场的风险测度是风险管理问题中的一个重要课题,在市场风险测度中一个重要的指标就是方差和波动率,波动率在金融经济领域是一个重要变量,一直以来都受到学者和业界人士高度关注,研究波动率的一个重要目的是预测未来市场实际发生的波动率,以便更准确地对资产进行定价,对资产进行配置和风险管理。目前用于预测波动率的模型有很多,这些模型主要分为两大类,一类是以历史数据为依据,根据历史数据去预测未来的波动率,其理论依据是认为波动率存在聚类效应,而且波动率以连续方式随时间变化,即波动率的跳跃不常见,另外一个原因是波动率不是发散到无穷的,是在一个固定范围内变化,所以大家认为可以根据历史数据对未来波动率的情况做预测。Robert F.Engle 的自回归条件异方差模型(ARCH 模型)是比较典型的基于 历 史 波 动 率 模 型 。1986 年 ,Bollerslev 在 ARCH 模 型 的 基 础 上 进 一 步 推 广 ,Bollerslev 认为条件方差不仅是滞后残差平方的线性函数,还是滞后条件方差的线性函数,构成了广义自回归条件异方差 GARCH 模型,GARCH 模型可以更方便地描述了更高阶的 ARCH 过程。此后,Nelson(1991)在 GARCH 模型基础上加入了资产收益的非对称效应提出了 EGARCH 模型,该模型使用条件方差对数,去掉了对模型系数非负性的限制。GARCH 族模型在随后金融风险问题研究中应用非常广泛,如陈守东和高艳(2012)运用二元 N-GARCH 模型和二元 GED-GARCH 模型,对金融危机前后利率和汇率的波动溢出效应进行研究,研究发现 GED-GARCH 的预测效果更好,利率与汇率具有双向的波动溢出效应。此外,还有其他一些描述了金融时间序列波动率演变的方法,如随机波动率 SV 模型等。张世英和余素红(2004)等对比了 GARCH 模型和 SV模型,并基于国内市场数据分析发现基于 SV 模型计算的 VaR 更具有动态性和准确性。
第 2 章 基于波动率与尾部损失的风险测度与检验
2.1 相关概念界定
2.1.1 波动率
在风险管理中,经济学研究了大量不断变化的经济变量,例如股价、汇率、市场价值、利率、回报或金属价值。它们随时间的波动可能会给市场参与者的金融资产带来价格风险,在数量经济学中,波动率是价格风险的量化表现,波动率的大小体现了资产价格的风险水平。当资产价格变化剧烈,未来价格不确定较强时,波动率指标往往也会比较高。相反,如果资产价格的波动率水平比较低,说明资产价格变化不大,市场参与者对于该资产的价值预期趋同,该资产的风险也就相对较小。
2.1.2 尾部风险
尾部风险(Tail Risk)指的就是罕见事件(Rare Event)发生的风险,是指资产或资产组合从其当前价格中由于市场剧烈波动,超过正常水平的风险,一般指两倍或三倍以上标准差的风险。然而,由于投资者通常更关心意外损失而不是收益,尾部风险的关注点便集中在负面的、不好的事件的亏损值,一般资产管理人通常对涉及可能损害或破坏投资组合的损失的尾部持谨慎态度,而不是对超额收益的受益尾部持谨慎态度。
当发生罕见的、不可预测的重要事件进而引起股票价值大幅波动时,就会发生尾部风险事件。这些尾部事件通常被称为黑天鹅事件,它们可以在很短的时间内对投资组合的回报产生灾难性的影响。部分关于尾部损失的研究表明,尾部损失事件发生的可能性要大于人们普遍认知的可能性。
2.2 市场波动的理论基础
2.2.1 股价随机游走理论
目前,在对波动率的研究中,学者们普遍假设股票价格是呈现随机游走的,这种随机游走过程被称为布朗运动(Brownian Motion)。最初时,布朗运动被用来描述分子撞击悬浮微粒做无规则运动的过程。在布朗运动理论被提出后,法国数学家巴契里耶(L.Bachelier)运用该理论来形容股价的波动。与物理学中的布朗运动有所区别,当前股价的波动不仅受历史价格波动的影响,还受实时市场行情的影响。Bachelier 认为,在任何一个时间点,投资人都无法判断市场会涨还是会跌,对应每一个交易价格,都有同等数量的买家和卖家,而当前的市场交易价格是受到大多数市场交易者认可的。若存在其他市场主流意见,那么成交价将会被改变。因此,从这方面来看,Bachelier认为股票价格从任意时间点来看都是一个均衡价格,在这点上,涨和跌的预期概率是一样的。 Bachillier 的另一个推论是波动幅度与时间间隔长度的平方根成正比,这个推论可以大概被解释成观察时间间隔越长,股价波动越大。巴基利耶用详细的实证分析证实了他的想法,这在当前的股市情形下还是有一定的适用性的。
2.2.2 有效市场理论
Eugene Fama 在 1970 年提出有效市场理论(EMH),有效市场假说是金融市场中套利定价理论、资产配置组合理论、资本资产定价模型等理论的基础。有效市场理论 认为市场中的历史信息甚至内部信息都不能对未来资产价格起到预测作用,正因如此,资产价格的波动率也是没有规律的,资产价格的变化过程可以看成是一个随机过程。但也有学者认为,随机的价格波动反映了一个高效性和功能性的市场,由于价格已经完整地反映了全部可能获得的信息,所以价格相对稳定,不存某一方向的趋势。假设市场参与者能够准确地预测未来股价而盈利,那只能说明股市无效率,即使通过对大批数据进行分析后,对股票市场做出某种正确的预测,其利润将被股票交易费用和各项分析成本所抵消。早期对于股价随机游走的研究,经济学家们只考虑了基于可观察的随机游走过程来分析股价序列的观点,并未对这些假设提供合理的经济学依据。Samuelson(1965)和 Mandelbrot(1966)在研究资产价格的过程中,认为资产价格的波动是在有效市场中参与者对于资产价格未来预期的不同而进行交易的结果,所以资产价格的波动在有效市场中有其存在的内在原因。
第 3 章 期权市场无模型隐含波动率的改进与实证分析 ........................ 37
3.1 无模型隐含波动率 .............................. 39
3.1.1 无模型隐含波动率法 ................................. 40
3.1.2 广义无模型隐含波动率法 ................................ 42
第 4 章 证券市场波动率和尾部风险的测度 .................... 63
4.1 波动率与尾部风险的关系 ............................ 64
4.1.1 历史仿真法 ............................. 66
4.1.2 参数法 ............................ 67
第 5 章 资本市场基于波动率和尾部风险的溢出检验 ............................ 80
5.1 尾部风险溢出的理论基础 ............................ 80
5.1.1 资本市场风险溢出成因 ............................. 80
5.1.2 资产价格风险溢出成因 ................................. 81
第 6 章 基于波动率和尾部风险的资产配置
6.1 资产配置与风险管理方法回顾
6.1.1 马科维茨均值-方差理论
现代关于风险资产配置的研究理论主要基于马科维茨均值-方差理论,该理论假设市场参与者都是风险厌恶的,在给定两个提供相同预期回报的投资组合中,市场参与者倾向于选择风险(方差)小的组合。因此,只有通过更高的预期回报补偿,投资者才会承担更高的风险。 从另一个角度,市场参与者想要更高预期回报,则必须接受更多风险。这意味着,在同等预期收益的水平下,理性的市场参与者会选择风险最低的那个组合。马柯维茨正是从理性参与者的这个资产配置问题,通过数学方法构造了均值-方差模型(Mean-variane Portfolio Model)。
马科维茨模型的建立是基于几个假设条件之上的,除了之前提到的市场参数者都是厌恶风险的假设外,其还假设各类资产的收益率是服从正态分布的,以及各资产的预期收益率、波动率以及协方差系数都是可以明确给定的等。这些假设在随后也遭到了很多学者和风险管理者的质疑。例如有很多学者基于不同市场的实证研究,否定了收益率服从正态分布的假设,最具代表的就是极值理论,极值理论认为资产价格收益率的分布呈现尖峰肥尾的形状,而不是标准的正态分布:还有学者基于行为金融学的理论指出风险资产的向上波动率和向下波动对于市场参与者的感受是不一样的,马科维茨模型中将具有对称性的方差定义为风险,但事实上,市场参与对于资产上涨和下跌的感受是非对称的。
第 7 章 总结与展望
7.1 研究结论与启示
本文通过对我国资本市场波动率与尾部风险的研究,基于市场有效性理论,认为随着资本市场的完善和信息技术的发展,信息在资本市场中的传递效率增强,在当前背景下,使用传统的历史数据,特别是历史低频数据,对风险预测和风险控制很难起到较好的效果。考虑到期权市场的价格数据,不仅包含对于历史情况的评估也包含了市场参与者对于未来的预期,且我国期权市场以专业的机构投资者为主,对于市场的判断相对更加准确。基于以上原因,本文使用我国期权市场的价格数据分析了无模型隐含波动率在我国市场的适用性,并基于无模型隐含波动率构造了资本市场的风险测度以及尾部风险测度,并利用构造的风险测度进行了资本市场的风险溢出分析和风险配置方法的研究,得出了一些有益的结论和政策建议。主要结论如下:
(1)本文提出的结合我国期权市场情况进行调整的广义无模型隐含波动率方法为我国资本市场未来已实现波动率的预测提供了一个新的指标,对投资策略和风险管理起到一定参考作用,并对我国的投资者和风险管理者还有研究工作人员提供了另一个可以参考的投资者情绪指标。针对我国期权市场,在单变量回归分析和信息包含回归的实证分析中发现,用指数模型对无模型隐含波动率方法进行补充后得到的波动率指标对未来已实现波动率的预测是有效的,预测效果强于历史波动率以及以 BS 公式用平值期权推导的隐含波动率,且从单变量回归分析模型中的 wald 统计量和系数发现无模型隐含波动率预测指标的无偏性相对更好,其中调整后的无模型隐含波动率相对于未调整的无模型隐含波动率的解释效果更强,改进后的无模型隐含波动率更适用于我国的期权市场,预测效果更好。
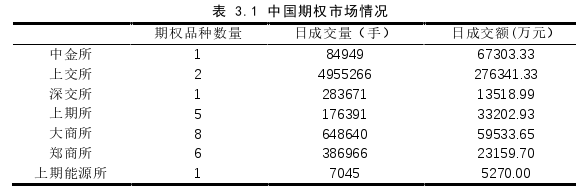
(2)由于我国的期权市场在刚刚起步阶段,市场的流动性不是很充足,对于同一标的的期权品种由于交易规则不同等原因,其流动也会存在差异,反映在期权价格中,就会导致一些流动性不高的期权品种存在一定的流动性风险溢价,由于较高的期权价格,导致根据该期权合约反推出的隐含波动率相对偏高。由于上证 50 指数和沪深 300指数都是代表国内偏价值类股票,而且两个指数在成分股中存在一定重合,且市场中存在对波动率进行套利交易的投资者使得我国期权市场中上证 50ETF 期权和沪深 300指数类期权之间的隐含波动率相关性较高。
参考文献(略)
