本文是一篇高校毕业论文,本文中对 EFM 中探针的模型过于理想化,锥形探针参考了 Sacha 模型,更多的研究了探针针尖对探测信号的影响。而实际上探针躯干、悬臂梁等结构也在一定程度上影响了参测结果。
第一章绪论
1.1 引言
纵观古今,人们对世界的认知离不开人们的各种感官。通过视觉、听觉、触觉、嗅觉等各种感官的相互配合,一点点探索着未知的世界。但人类自身的感官是有极限的,随着科学技术的发展,我们的各种感官已经不足以支撑我们对未知的探索,因此各种辅助器件的产生显得尤为必要。望远镜的发明,使我们看得更远;电话的发明,使我们听得更远;汽车等交通工具的发明,使我们跑得更远。但科学的发展是从中间向两端无限延生的,各种望远镜的发明使得我们更加直观的了解了宏观宇宙,但微观宇宙的探索也显得尤为重要,这一领域则离不开显微镜。
说到显微镜,人们最初想到的都是初中生物所接触到的光学显微镜,它是通过物镜和目镜的相互配合,进行光学成像,将物体的形貌展现在我们眼前,也就是说,光学显微镜是通过增强我们的视觉来达到认知物体的目的。随着人们研究尺寸的变小,光学显微镜已经不足以支撑我们的需求了。而认知物体的方法有很多种,扫描探针显微镜(Scanning Probe Microscope,SPM)作为一种新型显微镜被研制成功,他与传统显微镜的工作法是不同。SPM采用探针来探测物体的形貌,由光学显微镜的视觉显像变成了触觉显像。
1.2扫描探针显微镜(SPM)的发展
1982 年,由 Binnig 和 Rohrer 发明的扫描隧道显微镜(Scanning Tunneling Microscope,STM)是最早出现的一种 SPM 技术[1-2]。该技术的发展在当时的科学界引起了巨大的轰动,因为这一技术直接使得表面科学这一研究领域有了巨大的突破,各种基于 STM 技术发明的显微镜层出不穷。也因为这一技术,仅仅时隔四年,两位科学家就获得了诺贝尔奖。STM 扫描样品时,通过检测探针与样品间的隧穿电流,从而表征出样品的形貌,所以要求样品必须导电。为了克服这一缺点,Binnig 等人于 1986 年研制出了一种新型显微镜——原子力显微镜[3](Atomic Force Microscope,AFM),该显微镜通过检测和控制探针与样品间的作用力来成像,因此即使不导电的物体也可以使用该显微镜,从而扩展了 SPM 的研究范围。
接触模式:所谓接触模式,则是指在 AFM 扫描成像过程中,探针针尖与样品表面紧密接触,此时作用力表现为排斥力,导致悬臂梁发生弯曲,如图 1.3 所示。而悬臂梁的弯曲程度与作用力成正比,因此光电检测器接收到的激光点的位置可以等效的表现为探针样品间作用力的大小。当 AFM 扫描样品表面时,由于样品表面的起伏导致了悬臂梁弯曲程度的不同,为了使探针样品间作用力保持不变,即光电检测器接收到的激光点的位置保持不变,需要对悬臂梁进行上下调整,直到光电检测器接收到的激光点回到原来的位置。不难发现悬臂梁的上下起伏刚好反映了样品表面的上下起伏,通过监测悬臂梁的位移便可以得出样品表面的形貌。因此说接触模式是三种模式种最直观的检测样品表面形貌的模式。但由于接触模式中针尖与样品表面紧密接触,对于较软的材料,AFM 在这种工作模式下扫描时会刮擦样品从而导致样品的损坏。
第二章 金属材料的 EFM 探测信号分析
2.1镜像电荷法
2.1.1 静电场唯一性定理
空间内一个点电荷的电荷量以及位置确定后,其空间电场的分布恒定且唯一[17]。如果这个空间有界,且边界上的电势、电位移矢量确定,其空间电场分布也可以被唯一的确定。这一定理也说明,有界空间外的电荷对该空间内电场的影响完全体现在该空间的边界上,只要该空间内的电荷分布确定且该空间的边界上的电势以及电位移矢量确定,无论空间外的电荷分布怎么变化,空间内电场分布唯一。
通过唯一性定理,在求解空间中电场分布时,不需要直接求解复杂的拉普拉斯方程、泊松方程,通过其他任意方法得到解,只要该解满足泊松方程、边值关系和给定边界条件,那么这个解便是唯一的正解。
2.1.2 镜像电荷法主要内容
当我们在利用 EFM 扫描样品时,主要观察的是探针与样品间静电力的变化。由于样品表面不均匀等原因导致电势分布不均匀,随着探针的扫描,通过控制施加在探针上的电压,使探针样品间静电力保持一恒定值,从而得出样品表面电势的变化。因此得到探针到样品表面静电力的变化值是解决这一问题的关键。可以将 EFM 探测样品表面这一过程等价为图 2.1。
因为 EFM 工作在抬升模式下,因此我们只需要考虑库仑作用,而对于 EFM 扫描样品时,其静电力主要产生在探针针尖与样品表面。因此只需要分析探针针尖与样品表面的静电力。对于如图 2.1 所示的模型,探针针尖由针尖头与针尖驱赶两部分构成,整个针尖是一个轴对称模型,表面电势处处相等。当我们对探针施加电压时,探针内部电荷可以等效为中线上的一个个点电荷的集合。为了计算探针针尖到样品表面的静电力,即计算针尖与样品间的库仑力。我们需要知道该空间中的电场分布,在理论分析中,样品通常假设为无限大,此时可以将整个空间看做两部分,样品上表面之上部分和下部分。
2.2ABAB 型结构静电力分析
超晶格是在 1970 年由美国 IBM 实验室的江琦和朱兆祥提出的,是一种由两种晶格匹配很好的材料交替生长的周期性结构。在这种结构中,当电子沿垂直材料的方向运动时,由于两种材料的电学性质不同,电子的运动速度也会周期性的变化,造成震荡并制造微波,因此这种结构多广泛用于微波器件。在本小节中,我们主要讨论了超晶格材料电学性质,分析其ABAB 型(材料 A 的介电常数小于材料 B)结构与 BABA 型结构间的差异。
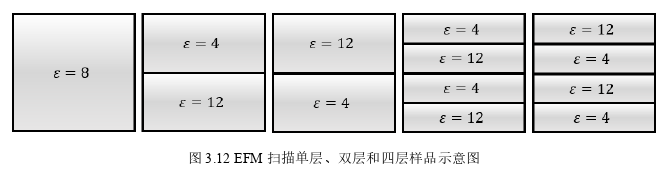
图 3.12 中分别展示了单层双层以及四层材料对应的模型,用 EFM 扫描时对应静电力非别为1F 、2F 、3F 、4F 、5F 其中单层材料厚度为 20nm,双层材料每层厚 10nm,四层材料每层厚 5nm,我们通过上一节中推导的公式分别对上述五种模型分析并利用 MATLAB 编程仿真,得出结果表 3. 1,并绘出图形如图 3.13 所示。
第三章 电介质及半导体材料的 EFM 探测信号分析........................20
3.1 镜像电荷法应用以及格林函数分析推导 ......................20
3.2 EFM 探测电介质样品信号分析 .....................20
第四章 探针形状对 EFM 信号影响的定量分析 .......................30
4.1 不同探针尖端对探测信号影响 .......................30
4.2 不同探针半锥角对探测信号影响 ......................30
第五章 总结与展望 ...................................45
第四章 探针形状对 EFM 信号影响的定量分析
4.1 不同探针尖端对探测信号影响
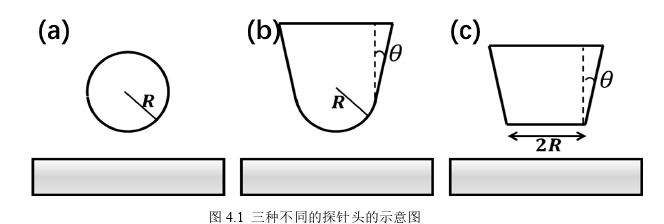
在用 EFM 探测样品时,EFM 需要扫描两次样品,第一次扫描时通常工作在敲击模式下,随着 EFM 使用次数的增加,这种工作模式会对 EFM 探针造成一定的磨损,通常磨损了的探针尖端会被磨平,此时在利用 EFM 探测样品时,产生的信号也许会与崭新的探针产生信号不同,从而造成探测结果的不准确。在之前人们对 EFM 探测样品的模拟分析中,通常将 EFM探针设为球心探针,而一般情况下 EFM 探针通常为锥形,在本小节中,我们主要研究了三种不同形状的探针探测样品时的静电力以及力梯度变化,同时也分析了探针参数对静电力变化。
第五章 总结与展望
本论文对 EFM 探测样品时产生的信号进行研究,从样品材料和探针形状两个方向出发,分析不同样品以及不同探针对探测结果的影响。通过镜像电荷法确定了不同材料对应的格林函数,并得到 EFM 扫描样品时产生的静电力的表达式,分析 EFM 扫描不同材料样品时产生的信号变化并解释其原因。其次,分析了不同探针形状对探测信号的影响。最后对开尔文模式下的 EFM 探测信号做了简单分析,研究探针灵敏度与本征频率、弹簧常数和品质因子间的关系,并通过噪声分析计算了调幅(AM)和调频(FM) 模式的灵敏度。本文的主要结论如下:
(1)探针内部点电荷的位置不影响仿真结果且 EFM 扫描金属样品时产生的静电力与 D 呈线性关系,其中 D 为探针样品间距。基于静电场唯一性定理,可以对球形探针扫描样品时内部等效电荷的位置及大小进行计算,发现当等效电荷增加到三个时位置不再发生变化且几乎不再影响扫描信号,利用镜像电荷法确定探针内部点电荷以及对应镜像电荷的唯一和大小。
(2)EFM 扫描电介质材料时,静电力随材料厚度呈幂指数衰减,随材料介电常数幂指数增加,并且发现材料内部电势不再恒定且随探测位置的上升缓慢上升,而样品表面到探针间电势迅速上升至0V 。而后,我们将样品材料拓展到多层,推导出 n 层电介质材料对应的格林函数并分析其在 EFM 探测时的信号变化,发现最上层材料对静电力信号的影响最大,但当最上层材料的介电常数较小时,下层材料由于其更大的介电常数可能会对最终信号产生一定的干扰。最后,研究了 EFM 探测半导体材料时的信号,分析载流子浓度对信号的影响,发现样品介电常数和厚度一致时,半导体材料对应静电力明显比电介质材料更大。
(3) 钝锥形探针扫描样品时会造成很大的误差。相比球形探针和锥形探针,当样品为金属且保持探针样品间距 D 为 1nm 时,钝锥形探针探测样品时产生的静电力是球形探针和锥形探针的 6 倍,并且该静电力随曲率半径呈平方变化,而锥形探针和球形探针产生的静电力随曲率半径线性变化。更大半锥角的探针会使得 EFM 扫描样品时产生的静电力更大,但相比探针尖端是否磨损,这个变化很小。通过这一结论可以通过分析 EFM 探测样品时产生的力信号判断探针是否磨损。
参考文献(略)
