本文是一篇学术论文代写,本文阐述 SOP 原理并建立应用于配电网规划的 SOP 数学模型;以 DPV 准入容量最大为目标,提出考虑改进安全边界和主动管理策略的DPV与SOP有功-无功协同优化配置模型;引入线性化近似将SOP模型等进行线性化,将原模型转化为混合整数线性规划模型,并采用 GAMS 进行优化求解。最后,基于某农网51 节点算例验证所提模型和方法的有效性和正确性,并分析安全边界、主动管理措施、SOP 容量对 DPV 最大准入容量的影响。
0 引言
高渗透率可再生能源的接入使得配电系统规划与运行面临着巨大挑战。一方面,大量分布式电源(DG)的接入会导致电压波动[1]、电压越限等安全问题;另一方面,DG规划配置的不合理、配电网调节能力的欠缺以及配电设备利用率低等严重限制了 DG消纳。而电力电子装备的大量接入使配电网呈现电力电子化的发展趋势,其快速发展为解决上述问题提供了新的思路[2]。
智能软开关(SOP)被用于代替多分段配电线路的联络开关,其功率连续无差调节特性可实现馈线间实时功率调动,改变系统潮流分布,提升配电网灵活性[3]。文献[4]研究了含 SOP 的多电压等级配电网运行优化;文献[5]建立了综合考虑 DG 有功-无功协同以及 SOP 运行的配电网鲁棒优化运行模型。文献[4-5]中的模型均考虑了 SOP 网侧运行进行配电网优化分析,采用 SOP 的非线性模型或将其转化为二阶锥形式进行问题求解,但非线性模型求解效率低。配电网规划人员可充分利用 SOP等灵活性资源进行主动配电网 DG 规划。目前关于 DG 规划的研究主要分为以下 2 类:一类以配电网经济性成本为目标进行 DG 优化配置,另一类则以 DG 准入容量最大为目标[6-11]。在经济性规划方面,文献[6]计及源荷关联场景建立以综合投资费用最小为目标的DG 规划模型;文献[7]建立以 DG 投资商收益、配电网公司收益最大化为目标的多场景 DG 规划模型。在准入容量评估方面,文献[8]提出考虑多种主动管理策略的三相不平衡配电网 DG 准入容量规划模型;文献[9]提出计及 SOP优化运行和其他安全约束的 DG 准入容量规划模型;文献[10]基于风电相关性场景建立以 DG 准入容量最大和电压偏移最小为目标的 DG 规划模型,用于评估配电网 DG 的最大准入容量。上述文献均基于典型日场景进行 DG 优化配置。随着光伏成本的不断降低,用户可在短期内收回光伏成本并获得收益。在我国碳达峰、碳中和目标下,当前研究重点是如何提升配电网分布式光伏(DPV)消纳能力。因此,本文计及 DPV 与负荷时序相关场景进行DPV准入容量的优化研究。
1 农村配电网安全边界
主动管理下考虑安全边界的柔性农村配电网规划思路如图 1 所示。传统配电网中无 DG 与主动控制手段,DG 优化配置时只考虑电压、电流等常规约束。随着电力电子化电力系统的发展,电网结构及运行方式发生变化,规划方式也变得更加复杂,但大多数规划方法只考虑正常运行下配电网对 DG 的消纳。而安全边界理论考虑了 N-1状态下配电网的运行状态,这对提升规划方案的可靠性具有重要意义。因此,本节重点阐述改进安全边界的数学表示及其在农网规划中的应用。
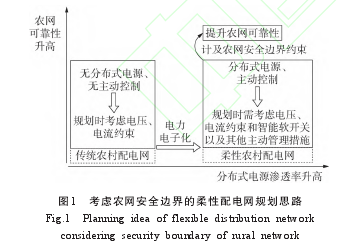
2 SOP原理与应用建模
SOP 基于全控型电力电子器件实现控制,两端电压源型换流器(VSC)灵活多变的控制方式能快速准确地控制自身有功/无功功率流动,改善配电网潮流和电压分布。配电系统通常分为辐射状或环状网络,而接入 SOP后的配电网成为一种混合系统,灵活的控制方式使其既具有辐射状网络开环运行的特点,又具有环状网络高可靠性的优点[17]。SOP 控制方式有以下特点[18]。
1)灵活的有功/无功功率控制。两端 VSC可根据幅值和相位建立独立的电压波形,可完全控制流经直流线路的有功功率,两端可提供独立的无功功率。
2)瞬时独立电压控制。由 VSC生成的电压波形可在几毫秒内实现动态控制,从而实现电压瞬时控制。
3)干扰和故障的隔离。VSC 的瞬时过电压/过电流受控制策略的限制,所以馈线上的网络干扰/故障可通过VSC与另一侧隔离。本文以背靠背 VSC 为例进行研究,基本结构如附录 A 图 A1 所示[19]。在正常运行状态下,SOP 的变流器 VSC1用于实现对功率传输的控制,而 VSC2则是实现对直流电压的稳定控制,即采用 PQ-VdcQ 控制方式。此时 SOP两端节点类型均可视为 PQ节点,且由于中间直流环节的隔离作用,所以两端 VSC 的电压与无功功率相互独立。
3 DPV与SOP协同优化配置模型
针对配电网 DPV 消纳,本文研究基于安全边界和 SOP 协同配置的 DPV 最大准入容量优化问题。将 DPV 的安装容量、SOP 安装位置以及 SOP 的安装容量作为决策变量,考虑农村电网安全边界、主动管理策略等约束,提出以 DPV 准入容量最大为目标的DPV与SOP有功-无功协同优化配置模型。
4 算例分析
以改进的 51 节点我国某农村配电网为例进行仿真分析,系统结构如附录 A 图 A3 所示,算例数据如附录A表A1和表A2所示。系统基准电压为10 kV,基准功率为 1 MV·A。系统中总负荷为 6 875+j2 440kV·A,共有 3 条馈线。假设 DPV 接入位置为节点32、34、43、47;SOP 待选位置为 5 个传统联络线位置;逆变器功率因数下限为 0.9;SVC 的安装位置为节点 14、48,可调范围为-500~500 kvar;SCB 的安装位置为节点 9、31,共安装 5 组。根据历史数据统计获取该地一年负荷、光伏出力曲线,如附录 A 图 A4所示。根据联合时序场景处理方式,将全年 8 760 h原始数据处理为 365 个源-荷联合时序场景,再根据3.4 节所提流程聚类为 9 个典型日场景,如附录 A 图A5所示。
需要说明的是,本文重点分析配电网 DPV 准入容量和 SOP 位置/容量协同优化配置问题,未考虑负荷增长、配电变压器升级改造等。
4.1 线性化参数优化结果
线性化参数优化结果本节通过修改式(48)—(50)中 κ 的取值,基于求解结果优化得到线性化参数 κ 的合理取值。此处仅考虑 DPV 与 SOP 协调规划,不考虑其他主动管理手段。线性化参数 κ的取值(线性化次数)和 DPV 规划结果、计算时间的关系如图4所示。
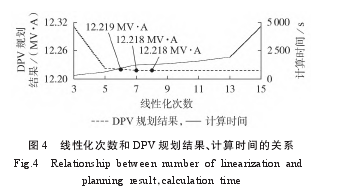
4.2 DPV准入容量优化结果
为考虑 SOP 安装的经济性,本节假设 SOP 的总安装容量不超过1 MV·A。
1)农网安全边界对DPV准入容量的影响。
本节主要研究农网安全边界对 DPV 准入容量的影响,优化配置结果如表 1、2 所示。由表可知,考虑农网安全边界的 DPV 最大准入容量结果略小于不考虑安全边界的,这是因为农网安全边界约束的加入缩小了原有数学模型的可行域。农网安全边界是考虑 N-1 安全的约束,能够确保优化配置结果在全场景运行下电网都在安全运行范围内,相较于不考虑安全边界的模型,其求解结果更加准确可靠。此外,SOP 优化位置一致但容量配置略有不同,说明农网安全边界的加入对 SOP的优化配置也具有一定的影响。
将上述 2 种情况下计算得到的全场景节点电压与电压基准值进行比较,各个场景下所有节点的平均电压偏差如附录 A 图 A6 所示。不考虑农网安全边界时全场景下的各节点平均电压偏差为 0.686 %,而考虑农网安全边界后各节点平均电压偏差为0.679 %。结果表明考虑农网安全边界有助于改善配电网电压分布,进一步表明考虑农网安全边界的有效性。
5 结论
针对高渗透率可再生能源消纳问题,本文提出基于安全边界和 SOP 协同配置的配电网 DPV 准入容量优化方法,提出考虑 SOP优化运行、农网安全边界和主动管理策略的 DPV 与 SOP 有功-无功协同配置模型,并基于线性化近似将其转化为混合整数规划模型,通过改进某农网 51 节点系统进行算例分析,得到如下结论。
1)采用线性化近似后,求解精度随着线性化次数的增加而增加,但计算时间随线性化次数增加呈指数增长。综合考虑计算精度和时间,本文将线性化参数κ设置为7。
2)考虑农网的网损后,农网安全边界相比城网安全边界发生变化;农网安全边界会影响配电网DPV 和 SOP 优化配置结果,且能够确保优化配置结果在全场景下电网都在安全运行范围内。
3)主动管理措施和 SOP协同应用可大幅提高配电网 DPV 最大准入容量,SOP 的提升效果相对其他主动管理措施效果更佳;当 SOP 安装容量上限达到一定程度后,限制 DPV 容量的因素是电压和馈线容量。随着可再生能源渗透率的不断提高,配电网的不确定性将增大。此外,大量电力电子设备的接入也使配电系统变得越来越复杂。如何处理规划模型中的不确定性和复杂性,如何考虑负荷增长、配电变压器升级改造等进行配电网拓展规划是笔者下一步的研究方向。
参考文献(略)
