本文是一篇物流论文,本文仅考虑了距离对电量消耗的影响,未考虑车辆在加速阶段的电量消耗以及减速阶段的动能回收,这与实际情况不符,今后需考虑在变速状态下的电池耗用情况。
第一章 绪论
1.1 选题背景及意义
当前,为顺利实现“双碳”目标,我国政府正主动做出战略决策,积极推动发展方式转变,加快构建绿色低碳循环发展的经济体系。在这一背景下,推动绿色物流发展是增强高质量发展的内生动力之一。绿色物流不仅可以实现物流整体系统最优化,还能降低对环境的破坏,对协同推进生态环境高水平保护和经济高质量发展具有重要的现实意义。为了实现高效的绿色物流,首先,需要合理规划物流配送网络,减少车辆行驶路径和温室气体排放;其次,作为运输载体的车辆可以选择新能源汽车替换为传统的燃油车,尤其是商业化程度最高的纯电动汽车。根据公安部统计的数据显示:截止到2021年底,我国新能源汽车保有量达784万辆,占汽车总量的2.60%。其中,纯电动汽车保有量640万辆,占新能源汽车总量的81.63%。
从政策层面来看,我国政府部门出台了各种鼓励新能源汽车发展的政策,包括财政补贴、税费减免、充/换电基础设施建设等。从物业配送企业层面来看,首先,纯电动汽车以其零排放、低污染等特征能够有效地降低环境污染,为绿色物流的发展提供有力支撑;其次,与传统燃油车相比,纯电动汽车在日常维护和保养方面具有显著的成本优势,且购买纯电动汽车免征车辆购置税,能够为物流配送企业节约一定的资金支出。
1.2 国内外研究现状
目前,国内外学者对电动车辆路径问题进行了大量的研究,取得了众多成果。本节对电动车辆路径问题的研究现状进行阐述,并对模型求解中所运用的算法的研究现状进行阐述。
1.2.1 车辆路径问题模型研究现状
考虑到纯电动车辆路径问题是由传统的车辆路径问题衍生而来,本节将从传统VRP、EVRP以及结合客户满意度的VRP三个方面阐述研究现状。
(1)传统VRP研究现状
车辆路径问题在交通运输、供应链管理等研究领域一直都是一个热点问题。最初由Dantzig和Ramser(1959)[1]提出,经过若干年的发展,车辆路径问题逐步演变成以下几种类型:
1. 多车型VRP,其关注的焦点是如何确定配送车辆的数量和类型以满足客户需求,从而达到营运成本最小。随着节能减排的政策持续推进,电动车等新能源车逐渐被应用到物流配送中,因此对多车型的车辆路径问题的研究十分必要。Deng等(2018)[2]研究了带时间窗的多车型VRP问题。Liu等(2016)[3]研究了异构运输车队的车辆装载问题。
2. 带多个时间窗VRP,具体表现为:每个客户点存在多个时间窗口,车辆可任意选择其中一个时间窗口进行配送。李珍萍等(2015)[4]提出了多硬时间窗VRP模型,对于服务时间要求松弛的客户点,Cao等[5]研究了多模糊时间窗的VRP。
3. 同时取送货VRP,在传统的VRP中,配送车辆只负责派送,但现实会遇到送货的同时需要取货的情况,如快递公司不仅要派发快件,还得从客户手中取走寄送的快递。Majidi等(2017)[6]、Wang等[7]建立了硬时间窗约束条件下的取送货车辆路径问题,Montero等(2017)[8]和Kalayci等(2016)[9]则从算法的角度进行研究,分别提出整数线性规划方法和混合算法对该问题进行求解。
第二章 基础理论概述
2.1 纯电动物流车的相关理论
2.1.1 纯电动物流车的概念
电动汽车指的是以车载电源为动力并由电机驱动车轮行驶,满足各项道路安全、交通法规要求的车辆,具体可分为纯电动汽车、燃料电池汽车和混合动力汽车三种。纯电动汽车是指完全依靠可充电电池提供动力的汽车,而纯电动物流车就是应用于物流配送领域的纯电动汽车。根据国标GB/T15089-2001可以得知,纯电动物流车根据车辆总质量的不同可以分为三类,其划分的标准以及具体车型如表2-1所示[56]。
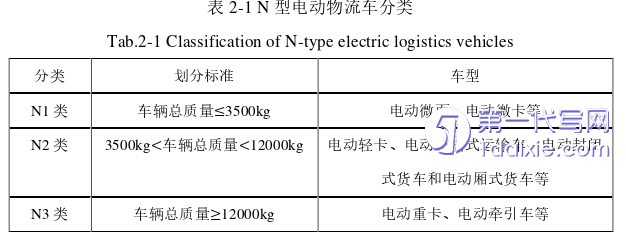
目前,第三方物流公司、搬家公司、互联网电商平台公司为响应国家节能减排的要求,均在探索并尝试使用纯电动车作为城市物流配送主要的运输工具。市场上最常见的纯电动物流车主要是N2类车型中的纯电动封闭式物流车和纯电动厢式物流车,它们的车厢容积在12至32立方米之间,载重量为1到1.5吨不等。
2.2 车辆路径问题理论
2.2.1 车辆路径问题概述
车辆路径问题自提出以来,一直是运筹学领域的研究热点。其定义通常可以描述为:满足一系列已知客户点的服务需求,对一定数量的车辆进行组织规划,合理安排每辆车的行驶路线,并在一定的约束条件下,实现诸如路程最短、成本最小、耗费时间最短等目的。
2.2.2 构成要素
车辆路径问题的基本构成要素包括以下六个部分:
(1) 配送中心
配送中心指的是从事配送服务的物流活动场所或组织,是运输车辆的起、终点,主要负责货物的储存、配置、装卸、搬运等任务。根据配送中心的数量可分为单配送中心和多配送中心。
(2) 客户点
客户点是配送车辆服务的对象,可分为送货点和取货点。不同的客户点对配送服务要求不同,具体表现为服务时间、需求或投递货物数量的不同。
(3) 道路网
道路网是指在一定配送范围内,由各种道路组成的网状道路系统,它连接了配送过程中的各个节点。配送过程中,车辆可能会遇到道路堵塞而无法及时送、取货的情况。
(4) 时间窗口
时间窗口指的是各个客户点可接受服务的时间段,在车辆路径问题中,可分为硬时间窗口和软时间窗口。硬时间窗口,配送车辆只能在客户规定的时间窗内到达,软时间窗口可以任意时间到达,但是需承担一定的惩罚成本。
(5) 约束条件
在车辆路径优化问题中,目标函数取决于设计变量,而设计变量的取值范围都有各种限制条件,而每个限制条件都可以通过函数的形式进行表达,这些函数表达形式则称为约束条件。
(6) 目标函数
在保证满足各种约束条件下,用设计变量来表示所追求的目标形式。目标函数可以是单目标函数,如行驶距离最短、车辆使用数量最少、总配送成本最低等;也可以是多目标函数,如在运输成成本最低目标下同时实现客户满意度最高等。
第三章 考虑配送及时性的纯电动物流车辆路径问题优化模型 ........................... 28
3.1 配送及时性的概述 ..................... 28
3.2 电动车充电策略 ................................. 28
第四章 改进的NSGA-Ⅱ算法原理 .................................. 35
4.1 改进的NSGA-Ⅱ算法 ........................................ 35
4.1.1 编码方式 .................................... 35
4.1.2 初始可行解生成.......................... 36
第五章 案例分析 ........................ 43
5.1 案例数据 ............................................ 43
5.2 求解结果及分析 .............................. 46
第五章 案例分析
5.1 案例数据
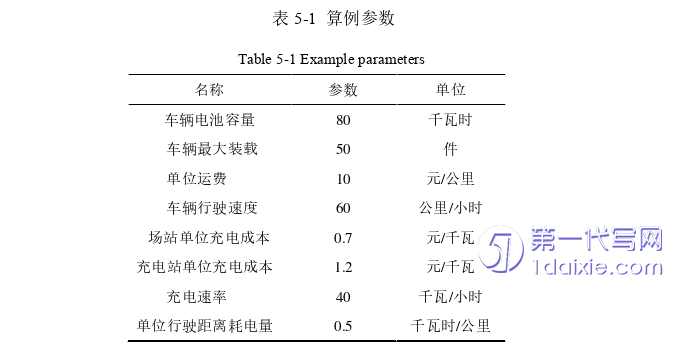
本文研究的主体是纯电动物流车的城市配送,故选择某新能源物流配送企业A作为研究对象,该企业已将配送车辆由传统的燃油车替换为纯电动车。随机选取A企业位于城区内的25个客户数据作为案例分析样本数据,为方便求解,本案例利用电子地图得到各点之间的最短导航距离,并形成客户坐标数据。同时,假定有10辆纯电动车可供差遣来完成配送任务。对于充电站,随机选择2个经常使用的充电站。算例的具体参数如表2和表3,客户信息详见表4。
实验环境,本文采用Matlab R2020a,相关参数设置如下:种群数=100,最大迭代次数300次,单点交叉概率为0.3,双点交叉概率为0.9,单点交叉变异概率为0.2,双点交叉变异概率为0.3,初始温度为500,降温速度为0.98。
第六章 总结与展望
6.1 全文总结
在追求“碳达峰”、“碳中和”目标的历史背景下,研究使用纯电动汽车代替传统能源汽车以减少配送路径中的碳排放,节约配送成本,对创建资源节约型、环境友好型社会具有积极意义。与此同时,随着政策支持的力度不断增加,纯电动车物流车凭借低污染、高能量转化率、拥有行驶路权等优势,逐渐成为解决城市配送需求的首选运输工具。但是纯电动车汽车充电时长、低温里程缩水、动力性能差、充/换电站布局等问题也制约了其在城市配送中的应用,因此实际运营效率并不高。为了提高运营效率,降低因配送不及时导致客户满意度下降的风险,本文着重考虑了平均客户配送及时度最大化和运输成本最小化之间权衡的问题并完成了以下研究工作:
(1)首先介绍了纯电动物流车的概念、特点、充电模式,总结了国内外纯电动物流车的发展现状,分析了纯电动物流车应用在城市配送中的影响因素及可行性;
(2)构建了客户配送及时性模型,通过车辆到达客户点时间的早晚,来判断配送的及时程度,从而量化了配送及时程度。在综合考虑了配送及时度和运营成本之间内在联系,建立了平均客户配送不及时度与运营成本(运输成本、充电成本)最小化的多目标优化模型,然后设计了改进的NGSA-Ⅱ算法对问题进行求解。
(3)对所构建的考虑配送及时度的纯电动物流车辆路径模型进行了实证分析。选取了某新能源物流企业的运营数据,利用MATLAB软件编写的算法进行求解,并与传统算法进行比较,结果显示,改进后的算法在四个维度都优于传统算法。同时分析了不同充电速率对运营成本与配送及时度的影响,结果表明,配送及时度与运输成本之间存在着制约关系,在充电速率较快的情况下,配送及时度从最小到最大的提升率高于运输成本的提升率,但是随着充电速率的加快,两者比值呈下降趋势。以上实验也验证了模型的有效性与可行性。
参考文献(略)
