本文是一篇电子商务论文,本文关于密度峰值聚类算法的研究工作到此结束,经过分析与总结,本文所提算法在聚类表现上要优于原密度峰值聚类算法,但是本文所提算法仍然存在着待改进的地方。
第一章 绪论
1.1研究背景与意义
互联网和信息技术的普及,促进了社会的经济发展,提高了人们的生活水平,也给各行各业带来了机遇和挑战。当代互联网技术已经与人们的生产、生活相互融合,成为人们生产、生活中不可或缺的部分,人们使用互联网进行工作、交流、游戏、网购等,也正因为如此,每天产生了数以亿计的互联网数据,这些数据反映了人们生活的需求。藏在这巨大的数据背后的信息价值[1] ,是推动整个社会经济发展、科技进步的关键。如何对这些数据进行获取、存储并挖掘出其中能被社会所利用的价值成为了当今社会信息处理的研究对象,数据挖掘领域[2] 也因此受到了人们的更多关注。
数据挖掘作为一门交叉领域的科目,受到广泛关注,其中一个常用的数据挖掘方法是来自与机器学习中无监督学习的聚类[3]。作为一种应用广泛的无监督学习方法,聚类已被应用于图像处理、数据挖掘以及模式识别等有着复杂结构的大型数据集[4-6]。聚类分析旨在对元素根据它们的相似性进行分类。聚类算法尝试将元素基于它们的相似性分为类别或集群,使集群内部成员相较于其他集群成员,在集群中彼此最相似。聚类理想的情况是当两个集群内部相似因子最大时,集群间的相似因子最小。
常见的聚类算法可大致分为以下几种:划分聚类[8]、网格聚类[11]、层次聚类[7]、模型聚类[10]、密度聚类[9]。层次聚类将数据根据相似程度以分层方式进行聚类。划分聚类将数据集划分成若干部分,每个部分代表一个簇。密度聚类将数据集根据其局部区域的密度、簇边界以及簇间连通性进行聚类。模型聚类使数据集与现有已知的数学模型进行拟合和优化并使用拟合和优化好的模型进行聚类。网格聚类将数据集所存在的空间划分为网格,并根据网格中数据的统计量进行聚类。
1.2国内外研究现状
本节将对现有的各种聚类方法进行介绍,并对密度聚类方法进行讨论,然后再对密度峰值聚类算法的研究现状进行讨论。
1.2.1 聚类算法国内外研究现状
对于聚类这一概念现阶段还没有非常精确的定义,因此研究学者们根据聚类原理的差别,将聚类算法大致分成网格型聚类、层次型聚类、划分型聚类、模型聚类、密度聚类等几种类型。
1、层次聚类
基于层次的聚类方法,使用自顶而下或者自低而上的迭代方式来划分簇。自顶而下的层次聚类方法为分裂层次聚类方法(Divisive),分裂层次聚类方法把每个样本点看作一个初始簇,通过迭代对这些簇进行合并,直到一个簇中包含了所有的样本点或者达到某些指定的终止条件为止。自底而上的层次聚类方法为聚集层次聚类方法(Agglomerative),聚集层次聚类方法先将整个数据集看做是一个簇,然后对已有的簇进行迭代划分,直到一个样本点为一个簇或者达到某些特定的终止条件为止。基于层次的聚类方法还可以进一步划分为:单连接(Single-linkage clustering)、完全连接(Complete-linkage clustering)、平均连接(Average-linkage clustering)层次聚类[14-16]。除此之外,科学家们也提出了一些为了改进层次聚类不足的算法,如为了能够更加有效的处理大型数据集BIRCH[17]和CURE[18]算法被提出;为了能有效处理分类数据集(categorical data),ROCK[19]问世。除此之外还有CHAMELEON[20]算法被提出。
2、划分聚类
基于划分的聚类方法将数据集进行迭代划分用以优化某些目标函数。最常见的基于划分的聚类方法如k-means[21]聚类方法,k-means聚类方法对簇中心与其他非簇中心样本点的某些距离尺度进行迭代优化。FCM算法[22],同样也是典型的基于划分的聚类方法,不同于k-means,FCM可以将样本点划分给多个簇。基于划分的聚类方法由于其简单、扩展能力较强且对于球形簇的聚类效果较好被应用于各种聚类应用当中,但是算法也存在缺陷,如需要人为指定簇的个数、对噪点敏感、对有不同密集程度簇的数据集聚类的结果不理想等问题。
第二章 相关理论背景
2.1 密度峰值聚类算法
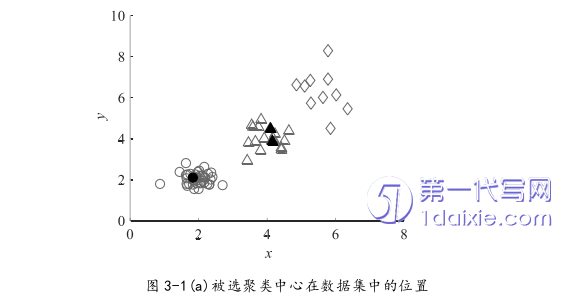
密度峰值聚类算法[12]是一种新颖典型的密度型聚类算法,相较于其他密度算法,密度峰值聚类算法对簇中心的确认需依赖于样本点自身的密度和与其最近的密度比其大的样本点的距离所建立的决策图,并需要在决策图上手动进行选取。下面对密度峰值聚类算法进行说明,本结公式均来源于文献[12]。
样本协方差矩阵通常运用于样本数量多,但是样本维度相对于样本数量少的数据集,在此种类型的数据集中,样本协方差矩阵通常能很好的反映样本数据集的真实协方差矩阵,误差较小,但当样本协方差矩阵被用于有着高维度的高斯分布的数据集时,样本协方差矩阵的表现将会下降。特别是当样本协方差矩阵被实际运用于处理样本数量多但是样本维度相对较少的实际数据集时会产生一些不尽人意的结果。在样本数量小于样本维数加一的数据集中,样本协方差矩阵是非正定、不满秩且奇异的,这就使得样本协方差矩阵不存在逆矩阵。即便是当样本维数接近于样本数量,并且样本协方差矩阵正定无偏时,样本协方差矩阵对真正的协方差矩阵的特征结构也是无法进行反映的,在这样的情况下,样本协方差矩阵的特征值会与真实协方差矩阵的特征值存在偏差。当样本维数接近于样本数量时,样本协方差的逆矩阵也不能真正反映真实协方差矩阵的逆矩阵。
2.2三支聚类
三支决策是二支决策模型的扩展,三支决策原理提出,人类在做决策时,需要使用所学的知识与经验作为决策的依据,但是,如果知识与经验不够充分,则在人做决策时不能得出确切的决定。因此,在知识与经验不充分的条件下做出的决定为临时决定,需要更进一步的对该决定进行判断。基于上述描述,三支决策的基本思想为,将全集分为3个不相交的部分,然后根据每个部分做出各自的决策。
三支聚类是由三支决策发展而来的[50]。三支决策是二支决策模型的扩展。三支决策原理是对人类决策方法的进一步表现。在没有足够的信息的情下,人们在通常不能够对某个决策进行肯定或否定,这些决策往往是模糊的,需要进一步的获取信息,才能够逐渐的将这些决策进行完善。因此对二支决策进行拓展,引出三支决策,将这些在当前情况下不能明确给出肯定与否定的决策,归到肯定与否定之外的决策,等待这些决策进一步的被完善。
在传统聚类算法中,簇与簇是互不相交的,一个数据样本点通常只分配给其中的一个簇,这样就导致了有着较近距离的簇的边界确定困难,这些距离较近的簇边界相互交融、重叠,不能够确定为具体属于哪一簇。簇的重叠区域的处理问题,存在于涉及数据挖掘的各个领域,是数据处理领域中人们关注的对象。常见的涉及簇重叠区域处理的问题有:某个产品同时属于多种类别的分类问题、具有常见症状的疾病的预测问题、社交媒体用户隶属于多个组别的问题以及对文本文档进行多标签分配的问题等[57-60]。
第三章 最优协方差密度峰值聚类算法 .................................... 17
3.1 密度峰值聚类算法密度计算存在的不足 .................................. 17
3.2 算法的基本思想与相关定义 ..................... 18
第四章 基于边界密度划分的最优协方差密度峰值聚类算法 .............................. 33
4.1 密度峰值聚类算法对簇重叠区域处理的不足 ................................. 33
4.2 算法的基本思想与相关定义 ............................ 33
第五章 总结与展望 ....................................... 42
5.1 总结 .......................................... 42
5.2 展望 ...................................... 42
第四章 基于边界密度划分的最优协方差密度峰值聚类算法
4.1 密度峰值聚类算法对簇重叠区域处理的不足
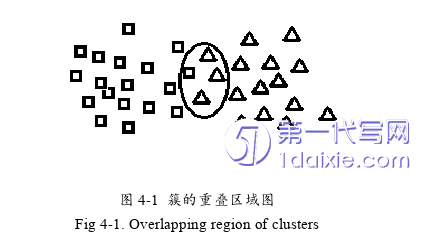
一个样本点所属于的簇,是由这个样本点在数据集中与簇的关系所决定的。根据数据集中样本点与簇的关系,可以是样本点属于单个簇,或者是样本点属于多个簇,或是样本点不属于任何簇。因此,定义样本点和簇的关系为:属于,不属于,和部分属于。样本点属于某个簇,意味着样本点是这个簇的组成成分。样本点不属于某个簇,意味样本点不是这个簇的组成成分。而样本点部分属于某个簇,则意味着样本点即是这个簇的组成成分,也是其他的簇的组成成分,这些有着部分属于关系的样本点,通常为簇与簇的重叠处。如图4-1所示,被划入圆形区域的样本点处于簇的重叠区域,他们在密度峰值聚类算法下只被分到其中一个簇,但是由于圈内区域样本的边界并不明确,在聚类时就很难对其进行合适的分配。
第五章 总结与展望
5.1 总结
为了对密度峰值聚类算法进行改进,提高其在实际运用中的聚类精确度和鲁棒性,本文首先介绍了密度峰值聚类算法的原理与流程,并分析了导致密度峰值聚类算法聚类不理想的原因。其中,密度峰值聚类算法的聚类结果很大程度上取决于算法的密度计算方式,也就是取决于截断阈值的选取问题。针对此问题,本文从相似度的计算着手,使用马氏距离代替欧式距离计算数据集中样本点间的相似度,并使用OAS协方差矩阵估计方法提高马氏距离的在高维度数据集中的适用性与精确度,在此之上将马氏距离结合k近邻算法,重新定义样本局部密度的计算方式,以此为基础在第三章提出了最优协方差密度峰值聚类算法,所提算法降低了密度峰值聚类算法对截断阈值的依赖性,使之能够在有不同密集程度簇的数据集中正确的找到簇中心,并提高算法聚类精度。
在第四章,本文着眼于密度峰值聚类算法对簇重叠区域处理不佳的问题。密度峰值聚类算法使用的是二支决策原理进行聚类,因此算法对簇重叠区域的处理往往不理想,本文引入三支聚类方法,将边界密度用于计算三支聚类的阈值,对密度峰值聚类算法的聚类结果根据三支聚类原理进行基于边界密度的划分并进行聚类结果的再分配,进而对密度峰值聚类算法的聚类结果进行进一步的优化,从实验结果可以看出,所提算法能够对簇的重叠区域中的样本点进行再分配并且能够识别出簇的重叠区域及其边界区域,在人工数据集和UCI真实数据集上有着较好的聚类效果。
参考文献(略)
