本文是一篇物流论文,本文分别建立了核酸样本采集选址-路径优化模型和核酸样本转运多目标路径优化模型,同时通过初始算例分析和参数敏感性分析来验证了模型合理性。
1 绪论
1.1 研究背景和意义
1.1.1 研究背景
新型冠状病毒肺炎(COVID-19,以下简称“新冠肺炎”)是由冠状病毒SARS-CoV-2引发的在全球大面积蔓延的呼吸道传染疾病,于2019年底和2020年初在我国湖北省武汉市初次进行大面积传播,导致数千人死亡和数万人感染。为此,中国政府制定了切实可行的防控政策以挽救人民群众的生命,各级政府自上而下严格落实。通过近两个月的艰苦努力,中国大陆地区新发病例增长得到有效遏制,截止2020年3月中国大陆地区的病毒传播链条已被正式切断,疫情被完全控制。相反,全球其他国家和地区的疫情却逐渐失控,从2020年1月份时仅有少数国家有确诊病例,发展到2月份出现少部分国家疫情确诊数据快速增长,疫情防控压力持续增加,再到3月份时病毒在全世界大部分国家和地区的人群中快速蔓延,2020年3月11日,世界卫生组织宣布此次新冠肺炎疫情成为全球大流行1。在新冠肺炎流行的两年多时间里,给全世界各国的经济发展、国民身心健康带来沉重打击,2020 年第一季度我国国内生产总值同比下降6.8%2,截至2022年2月,新冠病毒已导致世界各国和地区超过4亿人感染,超过580万人死亡3。

目前世界各国和地区的新冠肺炎疫情防控政策,大体可归为以下两类:第一类是中国、新加坡等国家实行的“类SARS防控策略”,也可称为阻断策略;第二类是美国、英国等国家采取的“类大流行流感防控策略”,也可称为缓解策略。阻断策略贯彻“早预防、早发现、早报告、早隔离、早治疗”的措施,对传染源进行严格管理,力图迅速切断病毒传播4。而缓解策略则强调对重症患者或有基础性疾病的患者进行重点关注,不注重所有患者的早期识别、轻症患者的隔离处理和患者及其密切接触者的排查与管控。从疫情防控效果来看,阻断策略实行国家的新发疫情得到有效遏制,病死率保持在较低水平;缓解策略实行国家的疫情传播持续发生,带来巨大的人财物损失。
1.2 研究内容
本文以新冠肺炎疫情常态化防控下需要高频、多点、突发进行大规模核酸检测为背景,在对核酸样本采集和转运优化问题进行系统分析后,通过查阅大量文献资料,构建了核酸样本采集选址-路径优化模型和核酸检测样本转运多目标路径优化模型,以求快速高效完成涉疫区域的核酸检测任务,最后通过初始算例分析和参数敏感性分析验证了模型合理性,给现实世界提供一定的管理启示。 本文共有六个章节,其中第一章、第二章和第三章共同构成本文的立题依据,第四章和第五章为本文的核心部分。各章节主要研究内容如下所示:
第一章为绪论。本章首先从新冠肺炎疫情对世界各国的严重影响、国内外主要防疫举措、核酸检测的意义、方式、流程和问题等方面出发,详细阐述了本文的研究背景,进而说明本研究的理论意义和现实意义。其次,本章按照本文的行文顺序叙述了各章节的重点内容。接着,本章阐明了本文的主要研究方法和论文创新点。
第二章为文献综述。本章主要介绍了基于成本最小、时间最短、公平决策和多目标平衡的国内外传染病应急物流优化相关,并对相关文献进行归纳总结和简要评述,为本文撰写提供文献支撑。
第三章为理论概述。本章重点介绍了传染病应急物流的基本概念、特征、运作流程,同时阐述了选址问题、车辆路径问题和选址-路径问题的区别、联系以及它们各自的特点、建模思路和求解方法,为本文撰写提供理论支撑。
第四章为模型构建。本章首先对大规模核酸检测样本采集和转运优化问题进行系统分析后,提出了模型的问题描述和基本假设。其次,本章结合运筹学、应急物流优化相关理论和数学建模方法,找出了模型的关键参数和决策变量。最后,本章以快速高效完成大规模核酸检测任务为目标,综合考虑现有检测资源、时间制约、居民出行限制等因素,构建了核酸样本采集选址-路径优化模型和核酸检测样本转运多目标路径优化模型。
2 文献综述
2.1 基于成本最小的国内外研究
国外学术界对应急物流和紧急配送相关研究开展较早,Kembal和Stephenson[1]最先将物流管理的相关理论和方法运用于突发事件中的物资调度,随后应急物流在突发公共事件领域不断拓展应用。成本因素一直都是优化研究的关注重点,在传染病疫情背景下,在疫情爆发前期可能会更加注重疫情防控速度,但当传染病疫情持续时间长、波及人群广、危害性大时,政府在做疫情防控部署时必须将成本因素进行重点考虑。例如,新冠肺炎疫情至今已持续两年多时间,我国疫情防控带来了大量的财政、个人和社会支出。应急物流优化领域的成本优化通常是一个系统概念,涉及选址成本、运输成本、分配成本、库存成本等众多成本项之间的相互影响和制约。
Ekici 等[2]与美国红十字会合作,研究流感大流行期间的食物分配计划。该文开发了一个疾病传播模型来估计疾病在空间和时间上的传播模式,将其与用于食品分配的设施位置和资源分配网络模型相结合,并开发启发式方法来为大型实例寻找近似最优解决方案。Jiang等[3]基于双层编程公式的思想提出了一种可变邻域搜索算法来解决在公共卫生事件爆发期间,居家隔离人员的快递配送最后一公里交付问题,目标函数是运输、分配和停车总成本。Zhang等[4]基于水波优化(WWO)元启发式和邻域搜索的混合算法,研究了在大规模疫情暴发情况下,可能有许多分散在不同地点的高危人群被转移到疫区进行医学隔离。针对高风险人群的个体转移,在可用检疫车辆数量有限情况下,研究新冠肺炎爆发地区转移医疗隔离高危人群的运输问题,使政府支出成本最小。Wolfinger等[5]提出在新冠肺炎检测过程中,通过移动检测队伍和固定检测队伍来收集核酸样本。该文通过构建混合整数线性规划模型,帮助政府决策固定检测点和移动检测点的位置和数量、各检测点对各疑似病例的服务时间、各疑似病例样本向各实验室的指派等问题,目标是让各检测点使用成本和移动检测点移动成本的总和最小。
2.2 基于时间最短的国内外研究
传染病疫情具有传播速度快、病毒变异性高、不确定性强等特点,因此在疫情爆发初期,必须采取快速高效的防控手段抑制疫情蔓延。在传染病疫情背景下,与时效性相关的应急物流管理研究主要集中在快速进行救援物资调度、感染者甄别、患者诊治等方面,而与时效性有关的目标函数设置主要有最小化关键响应时间、最小化最大响应时间、最小化期望响应时间等。
Özdamar等[14]提出了纳入自然灾害后勤决策与支持系统的规划模型,并解决了在持续援助项目的交付期间需要在给定时间间隔内重复处理的动态运输问题,以在紧急情况下尽快向受灾区运送救援物资。Wen和Zhao[15]从食品运输研究角度建立了配送路径优化模型,该模型能根据受灾地区的动态需求实时调整配送策略,以此不断提高应急管理背景下的食品配送效率。孙海等[16]构建了基于粒子群算法求解的随机网络应急救灾优化模型,该模型通过对应急救灾网络过程的量化分析,以实现救灾期望时间最短的目标。Zahedi等[17]开发了两种创新方法来设计救援供应链网络,即在新冠肺炎疫情大流行期间使用物联网来迅速发现潜在疑似病例。第一种方法(优先方法)使救护车的最大响应时间最小化,而第二种方法(分配方法)使总的关键响应时间最小化。每种方法都使用几个测试问题和伊朗的真实案例进行验证,结果表明所提方法在各种严峻新冠肺炎疫情大流行情况下具有良好性能。
3 理论概述 ........................................ 18
3.1 传染病应急物流概述 ............................. 18
3.1.1 传染病应急物流的概念及特征 .............................. 18
3.1.2 传染病应急物流的运作流程 .................................. 19
4 模型构建 ..................................... 26
4.1 核酸样本采集选址-路径优化模型 .................................. 26
4.1.1问题描述 .......................................... 26
4.1.2数学模型 ................................................. 28
5 算例分析 ................................. 35
5.1 核酸样本采集选址-路径优化模型算例分析 ........................... 35
5.1.1 算例初始数据 .................................... 35
5.1.2 算例初始结果 ................................. 37
5 算例分析
5.1 核酸样本采集选址-路径优化模型算例分析
5.1.1 算例初始数据
本节使用数据均属于基于实际情况的虚拟数据,且所有的时间单位都为小时(h),所有的距离单位都为千米(km)。具体数据如下:
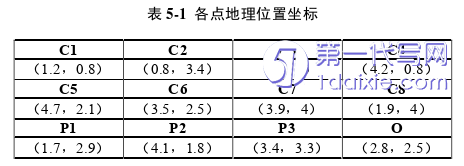
假设区域A需要进行全员核酸检测,该区域有8个需求点(代号C1,…,C8),3个候选固定采样点(代号P1,…,P3),4个移动采样点(代号K1,…,K4)。设所有固定采样点和移动采样点的起点站和终点站为同一个车站(起点站代号𝑂+;终点站代号𝑂−;车站代号O)。各需求点、候选固定采样点、车站的地理位置坐标见表5-1,地理位置分布见图5.1。设各需求点的待采样人数在区间[3000,10000]上服从均匀分布,利用MATLAB的randi函数随机生成。具体数据见表5-2。本节利用曼哈顿公式8计算两点之间的距离,通过距离除以旅行速度即可求出两点之间的旅行时间。设从车站到各固定采样点和各移动采样点移动均采用车辆行驶方式,而居民从需求点到固定采样点采用步行方式,其中车辆行驶速度为40km/h、行人步行速度为5km/h,各点之间相应旅行时间见表5-3、表5-4和表5-5。模型中其他参数的赋值见表5-6。
6 结论与展望
6.1 研究结论
在对大规模核酸检测样本采集和转运问题进行系统分析、查阅大量文献资料后,本文分别建立了核酸样本采集选址-路径优化模型和核酸样本转运多目标路径优化模型,同时通过初始算例分析和参数敏感性分析来验证了模型合理性。研究主要结论有以下两点:
(1)在模型合理性方面:对于核酸样本采集选址-路径优化模型而言,在初始算例设置下,该模型能在合理时间内完成采样点布局和需求点指派决策,总采样台数量约束、固定采样点覆盖半径约束和车辆路径相关约束均能得到有效满足。同时,结果显示所有需求点均能得到采样服务,且采样台数量更多的固定采样点承担更多采样任务,各采样点任务完成时间偏差率控制在20%以内,且总采样台资源利用率达到100%,显示了较好的求解性能。对于核酸样本转运多目标路径优化模型而言,在初始算例设置下,该模型能在合理时间内完成转运车辆路径规划和采样点指派决策,主目标模型和次目标模型均能满足实验室各评估批次检测能力约束、转运车辆配送周期约束和车辆行驶路径相关约束。同时,结果显示检测能力更强的实验室被分配了更多的采集样本,并且均能在第12个评估批次检测完所有样本,以此达到最小化总样本库存量和检测时间的目的。此外,从主次目标模型结果对比来看,在保证达到最低样本库存量𝑍1∗=27021的前提下,使得各转运车辆总行驶时间从主目标模型的1.98h减少为1.285h,节约了35%的运输时间,较好地优化了各转运车辆的行驶路径,证明了模型的合理性。
参考文献(略)
