本文是一篇电子商务论文,本文主要是以社团相依网络作为基本的研究对象,这个模型虽然能够体现很多现实世界的基本特征,但是也无法100%和实际数据完全相匹配。而我在阅读文献的过程中已经注意到当前学术界一个引发较多关注的模型或许可以减少这个误差,这就是多层网络模型(Multi-layer network[69][70][71]。它能将目前许多的网络模型囊括进来,在对不同孤立网络之间的相互作用进行刻画时,这个模型也更加多样和精确,所以其适用性也越高。
1.绪论
1.1 研究背景
现实世界是一个充满复杂性的世界,正是为了研究这种复杂性,基于数据的复杂系统的数学模型迅速发展成了一个新的研究领域:网络科学[1],这是一门典型交叉学科,涉及到数学、统计物理学、计算机科学以及其他专业领域。对于现实中典型的复杂网络,如因特网[2]、电力网络[3],交通网络[4]、全球公司股权控制网络[5]等,它们的结构、鲁棒性以及管控策略均可以借助不同的复杂网络模型予以研究。其中常见的经典复杂网络模型有ER随机图[6]、WS小世界网络[7]以及BA无标度网络[8]。上述网络模型偏重于复杂网络的理论研究,而为了达到特定的研究目的,使得复杂网络模型能够更好地描述现实世界的客观规律,学术界又进一步发展出了空间嵌入式网络(Spatially embedded networks)[9][10][11]、社团网络(Community networks)[12][13]等网络模型来刻画实际网络的主要特征。
作为本文研究框架内的社团网络结构主要是由于复杂系统中社团内的连边比社团间的连边更密集而产生的一种特殊的网络拓扑。大量的研究发现了包括生物网络[14],电力网络和因特网[15]、机场网络[16]以及金融网络[17]在内的许多实际网络都具有社团特征。而这种社团结构对于复杂系统的运行有着重要的影响,比如说,如今以微博、推特等为代表的社交媒体都是由众多的用户构成的,这些用户均可以看作复杂网络模型中的节点,并且用户之间相互关注账号、转发消息以及加入群组等等的活动都充分说明了网上社交系统的节点之间不是孤立的,那么可以将节点的这些相互联系看作是网络的相连边。同时也应该注意到这样建立的微博社交网络具有明显的社团结构,而正是这种社团特征的存在,使得社交媒体上新闻的传播比起名人效应受到更强的抑制[18],所以社团网络在研究特定系统规律时有着重要的现实意义。
1.2 国内外研究现状
社团结构是网络重要的拓扑特征,而将社团网络的独特规律运用到解决现实问题的第一步就是准确划分实际网络的各个社团。所以如何划分出实际网络的社团一直是学术界研究的热点[37],并且最近的研究已经将社团划分算法从单个网络[38]拓展到了多层网络[39]。这些算法可以大致分为两类:第一类方法是通过最大化模块度(Modularity)等目标函数来实现最优的社团划分[40];第二类方法则是使用随机分块模型(Stochastic block model)等概率方法[41]。另外,对于社团结构本身的研究也如火如荼,如Ya-Nan Bai等人[42]就通过同时引入失效机制和节点自我恢复机制研究了含有相依社团的网络的鲁棒性,文章发现在该模型遭受随机失效后对于很多不同拓扑结构的网络均存在一个突然的相变。如果这个相变点位于失效阈值之上,那么相依社团越大网络就会越脆弱,反之,相依社团越大网络就会越健壮。而Ghalmane等人的工作[43]则是针对非重合社团结构提出了三种免疫策略,并在SIR模型中证明了其相对于传统策略的有效性,但是文章为了更好地区分出影响力的节点也做出了许多假设,如连边的性质(社团内连边还是社团间连边)、社团的大小以及社团间连边的密度等。
除了社团结构外,相依关系也是关于复杂系统研究的一个重点[44]。比如Xingpei Ji等人[45]基于中国电网的特征提出了“Partial One-to-One Correspondence”相依网络模型,文章指出,中国的电力控制网络是受国家电网公司(输电网络)监测和管辖,所以每一个电站都会依赖于一个电力控制节点。同时,出于国家安全等原因,这个电力控制网络中存在着各个行政级别的控制中心以及光纤中继站等自治节点,他们都有备用电源所以不依赖电站供电。那么正是由于这些自治节点,文章建立了一个部分耦合的输电-通讯相依网络模型。而Run-Ran Liu等人[46]进一步拓展了相依关系的范围,文章假定不仅子网之间存在相依边,子网内部也存在相依耦合边,同时还假定一个节点只有一条耦合边,即一个节点不可能既与子网内节点相依又与其他子网的节点相依。文章发现当这两类相依边任何一个偏多时均会使得系统更加脆弱并且产生一个不连续的相变过程。虽然传统相依网络的研究方兴未艾,但是学术进展日新月异,2019年Danziger等人的研究[47]显示相依网络可以被包含在更广泛的多层网络模型之中。文章提出了一个动态依赖的框架来研究复杂系统的相依与竞争关系,并且通过这个多层网络模型取得了Buldyrev等人[19]在2010年最先提出相依网络模型时关于相变的一致结果。
2. 复杂网络相关理论
2.1 复杂网络的基本概念
目前学术界对于复杂网络(Complex network)的研究主要是基于图论(Graph theory),通过图可以清晰地表示复杂网络的拓扑特征(Topological property),反映网络的内在规律。图主要是由节点(Node)和连边(Edge)两个主要要素构成,两者之间的关系就是网络的节点通过边相连组成图形。另外,网络的拓扑特征只与节点个数和哪些节点之间存在连边有关,这也就意味着其他的因素(如节点的大小和位置)并不影响网络的拓扑性质。以此出发,可以将现实世界中的很多复杂系统抽象成含有点和边的图,并通过复杂网络相关模型来进一步研究其性质。其中,图的数学表示方法为:假定网络G是由节点的集合V和连边的集合E组成,即𝐺=(𝑉,𝐸),那么节点个数N和总边数L就可以分别表示为|V|和|E|。所以有𝑉𝑖∈𝑉,𝑖=1,2,… ,|𝑉|,(𝑉𝑖,𝑉𝑗)∈𝐸,𝑖=1,2,… ,|𝐸|。
在边集E中的连边可以分为是否有权(Weighted)和有向(Directed)。前者是指节点之间连边的强度,若以道路作为两个城市之间的连边,那么国道和省道显然在相同时间内通过的客流量就有差别,这就是连边不同权重值的差别。而后者主要是说对于节点集中的节点𝑉𝑖和𝑉𝑗,若将𝑉𝑖作为始点指向终点𝑉𝑖那么(𝑉𝑖,𝑉𝑗)就是一条有向边,反之,若是𝑉𝑗作为始点指向终点𝑉𝑖,那么(𝑉𝑗,𝑉𝑖)就是另一条有向边,并且(𝑉𝑖,𝑉𝑗)和(𝑉𝑗,𝑉𝑖)是属于边集E的两条不同连边。本论文为了简化研究但是不失侧重点主要是研究以无权无向图作为基础的复杂网络,也就是说在该网络中,不考虑节点之间的连接强度只考虑相互之间是否有关系,即(𝑉𝑖,𝑉𝑗)和(𝑉𝑗,𝑉𝑖)视为一条边,并且G中的节点不存在自环(self-edge),即(𝑉𝑖,𝑉𝑗)∈𝐸,𝑖=1,2,… ,|𝐸|,𝑖≠𝑗。那么,通过一定的节点和连边规则就可以构建出刻画现实世界的网络图,如下图2.1所示,以2019年12月31日A股公司和其前十大股东作为节点,并以他们之间的股权关系作为连边就可以构造出如下的无权无向图:
2.2 ER网络与SF网络模型
在一个具体的网络𝐺(𝑉,𝐸)中,设节点个数𝑁=|𝑉|,节点i的度为𝑘𝑖,i=1,2,3,…,N。如果将𝑘𝑖从大到小进行排序,那么我们就可以得到节点度为k的节点数占全部节点个数的比例𝑝𝑘。在下图2.2所示的孤立网络中,总共含有10个节点(𝑁=10),按照该网络的节点和连边关系,我们可以得到如下表2.1所示的每一个节点的度。
显然度分布是一种离散分布,因为随机变量k的取值范围为自然数,从而根据网络度分布的不同,我们可以推导出两类基本的随机网络模型:ER网络和SF网络。
ER随机图是Erdös和Rényi在上世纪50年代提出[6],此后一直是学术节研究复杂网络拓扑的理论基础。ER随机图有两种构造算法,一种是按照固定的边数构造ER随机网络,另一种是根据固定的连边概率构造ER随机网络。本文将采用第二种方式,因为目前大多数关于随机网络的研究都是以后者作为理论模型。具体的计算机生成算法为:
第一步:设在ER随机图𝐺(𝑁,𝑝)中,从其N个节点任意选择两个节点,并且这两个节点存在相连边的概率为p。
第二步:从N个节点中随机选择2个没有相连边的节点𝑉𝑖和𝑉𝑗并且𝑖≠𝑗;
第三步:生成一个在0和1之间的随机数r;
第四步:分为两种情况:𝑟<𝑝时我们在ER随机图中生成相连边(𝑉𝑖,𝑉𝑗)(或者(𝑉𝑗,𝑉𝑖));𝑟≥𝑝时就不在这两点之间生成连边;
3. 构建静态的社团相依网络模型 ................................. 21
3.1 独立社团网络的建构及分析 ................................. 21
3.1.1 社团网络的物理模型 .................................... 21
3.1.2 ER社团网络的数学模型 ............................... 22
4. 对社团相依网络模型的动态分析................................ 39
4.1 网络鲁棒性的评价指标 ..................................... 39
4.1.1 极大连通子图 ....................................... 39
4.1.2 极大连通子图系数 ................................... 41
5. 基于耦合关系的动态恢复策略 ................................. 76
5.1 相关恢复策略的比较 ....................................... 76
5.1.1 恢复模型 ........................................... 76
5.1.2 MSS恢复算法 ........................................ 88
5. 基于耦合关系的动态恢复策略
5.1 相关恢复策略的比较
5.1.1 恢复模型
针对共同边界节点的恢复模型是由Muro等人在2016年专门针对相依网络提出的网络管控模型[53]。该模型的关键是确定每轮级联过程中的共同边界节点,然后按照一定的恢复比优先将其部分恢复,这里说的恢复是指将失效共同边界节点按照初始网络的连边关系重新连入极大联通子图。
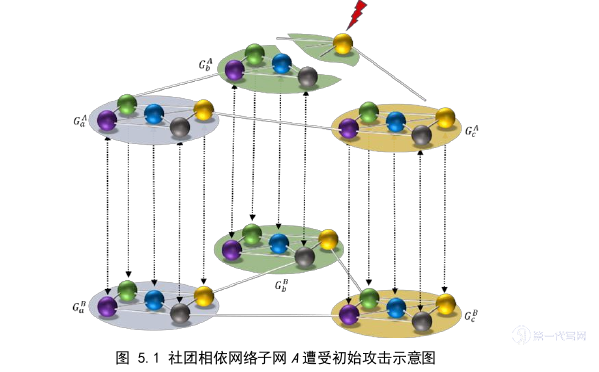
首先,假定有一个社团相依网络G如下图5.1所示,其中G含有上下两个子网A和B,每个子网含有15个节点(𝑁=15),而每个子网又分为三个社团(𝑚=3),分别以浅绿、浅蓝和浅黄三种颜色的椭圆表示。将耦合密度couple设定为1,如果两个子网内的节点一一对应耦合,也就是每个节点有且只有一条耦合边(以带双向箭头的黑色虚线表示),那么G总共有15条耦合边;同时又将噪音系数noise设为0,也就是G中三对社团一一对应耦合。
6. 研究结论和政策建议
6.1 关于对相依社团网络模型的研究结论
6.1.1 涉及的参数
本文在建立社团相依网络的过程中,涉及的主要参数有: 仿真实验的次数(Number of realization),由于本文主要是通过计算机仿真实验来对模型的级联过程和算法恢复效果进行研究,而实验次数越多取平均后就越能接近理论上的结果。所以本文同意固定模拟次数为1000次,这已经能较好的消除实验误差带来的影响,从而使得实验充分反映理论。
初始失效策略(Initial failure strategy),目前学术界在对社团网络级联失效的研究中主要是以针对桥节点的蓄意攻击作为初始攻击策略,但是本文不仅研究了在不同攻击策略下社团相依网络级联的相关规律和恢复效果,而且着重研究了能广泛反映现实情况的随机攻击策略。
子网的拓扑结构(Network topology),为了更加贴近现实世界,本文充分研究了两种不同度分布(ER和SF)的网络模型对于社团相依网络相关结论的影响。由于相依网络有两个子网,所以可以建立三种不同的社团相依网络(ER-ER,SF-SF,ER-SF)。
节点个数N(Number of nodes),节点个数越多,算法的时间复杂度会越高,同时当𝑁→∞时,网络极大连通子图存在的概率𝑃∞趋于理论值。
网络平均度k,本文研究了平均度对于社团相依网络结构以及级联过程的影响,并且比较了在不同平均度下的算法恢复效果。但是在对其他参数进行探讨的实验中,按照惯例[55]本文一直将子网的平均度固定为5。
社团个数m,社团个数属于网络的结构参数,m的变化会让网络的拓扑结构发生改变,而且两者之间的变化并非是简单的线性关系,本文着重研究了𝑚=2、10、100时社团相依网络的级联过程和恢复效果所发生的变化规律。本文除了研究社团个数m变化的实验外,均固定𝑚=10。
参考文献(略)
