本文是一篇物流论文,本文梳理了考虑最大时滞窗的装配流水车间生产配送集成调度问题的难点,以及两类不同布局装配流水车间调度的特点;分析了装配流水车间两种不同布局下,考虑最大时滞窗的生产配送集成调度问题的约束,构建了相应的数学模型,并通过CPLEX求解小算例验证了模型的正确性。
1 引言
1.1 研究背景与意义
1.1.1 研究背景
制造业的发展水平是一个国家综合国力以及工业化进程的有力标志,在一定程度上也是国家先进生产力的代表。但我国制造业仍存在调度水平低、总成本过高等问题,为了发挥产业优势、应对全球化竞争,响应中国制造号召,同时更好的适应市场变化、满足市场多样化、个性化需求,适应工业4.0趋势,制造企业的生产模式逐渐转变为多品种、小批量生产,面向订单生产(MTO)的模式成为制造企业的主要生产模式。如何充分利用资源,在有效控制成本的同时完成订单的高效履行,是制造企业面临的新课题。订单履行包括了从订单接收到订单生产和订单配送的全过程。
生产调度是生产计划与控制的核心[1],企业通过科学的生产调度可有效配置资源从而达到最大完工时间最小化、生产耗能最小和延迟成本最低等目的。但制造企业作为供应链中的重要角色,供应链上采购、生产、配送等各环节的协调和调度均会影响到企业发展[2]。尤其是在定制化生产模式和准时制生产模式下,企业为有效控制成本很少设置或不设置成品库存,使得产品的生产和配送环节联系更加紧密。订单履行时间由生产时间和配送时间两部分构成,配送环节受到生产环节订单完工次序和完工时间的限制,生产环节又受到订单到期日和配送计划的影响。因此,生产和配送环节单独管理难以实现系统整体运营绩效的优化。对制造企业而言,综合考虑产品在供应链上的生产和配送环节,进行集成调度是必然选择。供应链生产配送集成调度已经被广泛应用于食品加工、生物医药、化工、等各个领域[3]。经验证,生产配送集成调度可以显著降低制造企业运营成本,提高客户服务水平和资源利用率[4]。
1.2 研究内容及方法
1.2.1 研究思路
本文按照发现问题、分析问题和解决问题的总思路展开。通过文献研究与实地调研的方法明确装配流水车间生产配送集成调度问题的特点与难点,对生产环节中制约生产效率的瓶颈约束:最大时滞窗约束对集成调度问题的影响进行分析。通过对实际生产中常见装配流水车间布局分类的梳理和现有生产配送调度问题研究成果的评述,对现有研究中装配流水车间生产配送集成调度问题进行扩展,提出了本文的研究问题:考虑最大时滞窗的装配流水车间生产配送集成调度研究。区别于现有研究成果中考虑的传统Pm→1布局两阶段装配流水车间,本文以另外两类主流布局为研究对象,分别研究了DPm→1布局和Fm→1布局下生产配送集成调度问题,并考虑了两类情景中,制约实际生产效率的最大时滞窗约束。进一步,将该问题抽象为理论问题,运用运筹优化的思路提出了针对两种情景的集成调度模型,通过小算例求解验证模型的正确性和可行性;针对该复杂问题设计求解算法,采用该算法对不同场景中的算例进行求解。通过算例结果分析,给出相应的管理建议。
2 相关理论基础及文献综述
2.1 时滞窗
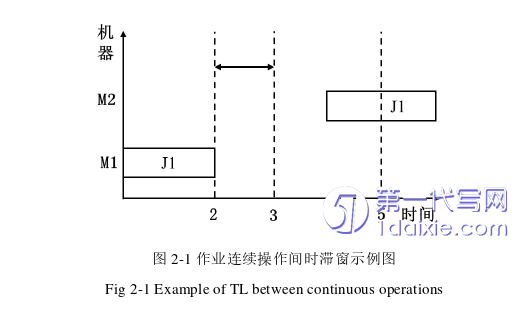
时滞窗是指作业两个连续操作之间、两个连续作业或者两个连续机器之间的时间间隔。比如:某一作业必须在特定作业结束后给定的时间范围内开始,或者某台机器必须在另一台机器开始工作后的一段时间内使用。时滞窗可分为三类,分别是:最小时滞窗(minimal time lag),最大时滞窗(maximal time lag)和精确时滞窗(exact time lag)[9]假定对于某个任务,其任意的连续操作之间存在最大时间窗和最小时间窗约束,这表明对应连续操作的上游机器操作结束和下游机器操作开始之间的等待时间是存在上下界的。而等待时间的上下界分别对应为最大时滞窗和最小时滞窗约束[10]。如图2-1所示。该图中,作业J1的两个连续操作之间最大和最小时滞窗分为5和3,因此该作业的第二个操作可在其紧前操作结束后,在此时间窗口内任意时间开始,而不违反时滞窗约束。
2.2 流水车间
流水车间(Flow shop)是指对应于不同的加工工件,有着相同的加工顺序,各工件的加工时间可以相同或不同。流水车间调度问题(Flow Shop Scheduling Problem,FSSP)是许多实际流水车间生产调度问题的简化模型,是一个典型的 NP 难问题,它也是目前研究最广泛的一类典型车间调度问题。流水车间可进一步细分为置换流水车间、非置换流水车间、装配流水车间以及混合/柔性流水车间。
2.2.1 置换流水车间
置换流水车间(Permutation Flow Shop PFS)是对流水车间的进一步约束,具有多工序串行加工的特点,对每个机器来说,工件必须按照相同的顺序进行加工。置换流水车间示意图如图2-2所示。如图2-2,作业J1,J2需在3台机器上进行加工,每个做作业有着相同的加工工序,每台机器上作业必须按照相同的顺序进行加工,每个机器同时只能加工一个作业,不允许抢占、不允许中断,同一作业同一时间只能在一台机器上加工。
2.2.2 装配流水车间
装配流水车间(Assembly Flow Shop AFS)是目前流水车间调度的主要方向。在传统的两阶段装配流水车间中,产品或服务的部件/组件/子集先在第一阶段并行加工,然后在第二阶段进行组装。一般形式可以表示为:第一阶段有L台并行机,每台机器可用于加工产品的每个部件,部件加工结束后,进入第二阶段的装配台进行装配操作。每台机器一次只能加工一个工件,每个工件同时只能在一台机器上加工。产品的部件数与加工机器数量无约束关系。
3 考虑最大时滞窗的装配流水车间生产配送集成调度问题分析与建模 ............................. 25
3.1 问题阐述与难点分析 ...................................... 25
3.2 考虑最大时滞窗的两阶段装配流水车间生产配送集成调度问题 ........................................ 28
4 GA-VNS混合算法设计 ........................... 41
4.1 GA-VNS混合算法框架及步骤 ........................... 42
4.2 染色体编码与解码 .................................... 43
5 算例设计与结果分析 ................................. 49
5.1 考虑最大时滞窗的两阶段装配流水车间生产配送集成调度算例设计与求解 ....................... 49
5.1.1 算例设计 .......................................... 49
5.1.2 参数设置 .......................... 50
5 算例设计与结果分析
5.1 考虑最大时滞窗的两阶段装配流水车间生产配送集成调度算例设计与求解
5.1.1 算例设计
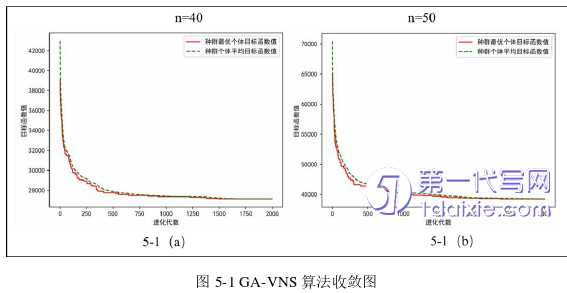
本节针对MTL-TAFS生产配送集成调度问题设计了两类算例。第一类算例18组:作业数n∈{5,6…10},车辆数V=3,机器数m=3,其中,两台机器为并行机,只能用于加工指定类型的部件,一台机器为装配机。作业各部件在专用机器上的加工时间和部件装配所需时间均在[1,8]的区间内随机产生;客户地点和工厂位置在10*10的正方形上随机选择,不同地点之间的距离类型为欧几里得距离;假设各点之间的旅行费用与其行驶时间相同;在每一类作业数量场景下,加工阶段与装配阶段间的最大时滞窗分别为3,11,20;其余参数随机生成。第二类算例63组:作业数n∈{20,21…30…40},机器数m=5,车辆数V随着作业数量的增加而增加,分别为V=4,6,8;客户地点和工厂位置在20*20的正方形上随机选择,不同地点之间的距离类型为欧几里得距离;在每一类作业数量场景下,加工阶段与装配阶段间的最大时滞窗分别为4,12,20;其余参数生成规则与第一类算例相同。以上各组算例分别进行10次实验,取10次实验结果平均值作为分析对象。
6 总结与展望
6.1 全文总结
本文以装配流水车间生产配送集成调度问题为研究对象,将生产环节存在的瓶颈约束:最大时滞窗约束纳入考虑,结合已有国内外研究成果,分别研究了两种装配流水车间布局下,考虑最大时滞窗的生产配送集成调度问题。即考虑最大时滞窗时的PFm→1布局两阶段装配流水车间生产配送集成调度问题和Fm→1布局多阶段装配流水车间生产配送集成调度问题。本文将其分别称为:MTL-TAFS生产配送集成调度问题和MTL-MAFS生产配送集成调度问题。其中MTL-TAFS布局中,加工阶段为并行专用机器;MTL-MAFS布局中为串联多用途机器。通过对加工阶段与装配阶段产品部件供需关系以及产品生产环节与配送环节依存关系的分析,针对不同生产配送集成调度系统特征,将产品生产环节不同阶段间存在的最大时滞窗约束纳入考虑,本文进一步从生产环节、配送环节、生产配送环节的关系等几个方面入手,考虑资源约束,构建了以供应链系统总成本最低的数学模型,并通过CPLEX求解小算例验证模型的正确性。由于本文研究问题为NP难题,本文将遗传算法和变邻域搜索算法结合起来,进行GA-VNS智能混合算法设计求解问题。最后针对两个模型分别设计81组算例,每组算例采用GA-VNS与CPLEX进行10次实验,对其平均求解结果进行分析,验证了GA-VNS算法对MTL-AFS生产配送集成调度问题求解的适用性和集成调度对降低供应链系统总成本的有效性,并分析了MTL-AFS生产配送集成度调度时,最大时滞窗约束的影响。
本文的研究成果主要如下:
(1)本文梳理了考虑最大时滞窗的装配流水车间生产配送集成调度问题的难点,以及两类不同布局装配流水车间调度的特点;分析了装配流水车间两种不同布局下,考虑最大时滞窗的生产配送集成调度问题的约束,构建了相应的数学模型,并通过CPLEX求解小算例验证了模型的正确性。
(2)本文设计并实现了混合GA-VNS算法,针对本文研究问题设计三层编码规则,并用GA迭代的最优解作为VNS的初始解,采用插入、互换、逆序操作构造邻域,进行随机搜索和局部搜索,避免陷入局部最优同时提升解的质量。 (3)本文对两个问题分别设计大小两类算例,每个问题共81组算例,每组算例进行10次实验。通过大量数值实验,验证了GA-VNS算法求解两类问题的适用性和在两类情形中,进行生产配送集成调度优化系统成本的有效性,并从问题求解难度、调度总成本两个角度对最大时滞窗对装配流水车间生产配送集成调度问题的影响进行了分析,得出结论:1)全部作业数量场景下,一般来说,设置最大时滞窗越紧,系统总成本越低;同时随着最大时滞窗增大,问题求解时间也增多;2)最大时滞窗对装配流水车间生产配送集成调度问题的影响程度随着作业数量的增多和时滞窗的紧缩呈增长趋势。在以上结论的基础上,为制造企业提出了相应的管理启示。
参考文献(略)
