第一章绪论
1.1选题背景及意义
随着科学技术的不断发展与进步,人们收到的大部分信息都来自于图像数据,正如成语“百闻不如一见”所表述。但是在形成、传输以及接收图像的过程中,被外界环境影响是不可避免的,图像质量必然会下降,这直接影响人们对图像信息的接收且它的效果和准确性值得怀疑,为了较好的获取图像信息,必须对其进行分析和处理,因此图像处理成为计算机应用研究领域的一个重要分支是必然的。数学形态学在图像处理理论和方法的研究中非常实用。比如与中值滤波、均值滤波以及维纳滤波等传统的图像去噪算法相比,它有很多突出的优点,例如在有效去除噪声的同时可以很好地保护图像细节特征、算法执行效率非常高等。在图像处理的过程中,传统数学形态学采用形状固定、大小固定、方向固定的结构元素,即对整幅图像进行一种统一处理,这样非常容易导致对图像的“过处理”或“不及处理”。是否在形状、大小以及方向上选择了合适的结构元素,将对图像的处理结果有直接的影响。所以为了更好地将数学形态学引入日益广泛的图像处理应用中,针对不同的应用领域、不同的图像局部特征来设计自适应的结构元素和处理算法是非常有必要的。SV数学形态学是目前较为流行的理论之一,其结构元素的选择与所处理图像的局部特征密切相关。SV数学形态学理论思想正式建立,可以追溯到1988年Serra提出的结构函数的概念及它的应用W,它不仅保留了结构元素的意义,而且为数学形态学理论框架引入到广泛的实践应用中奠定了坚实的基础。SV结构元素根据输入图像特征和被检测点局部邻域结构的特征变化而自动调整大小、形状和方向等。
……..
1.2国内外研究动态
数学形态学在1964年诞生,它是由法国巴黎矿业学院教授MatheronHi及其学生Serrai5i提出“击中/击不中变换”概念时引入的,这也是在理论上第一次引入形态学表达式,为该学科奠定了理论基础。1982年,Serra的《Image Analysis and Mathematical Morphology》t5i在计算机视觉、图像处理、模式识别等领域,引起广泛的应用与重视。在过去的几十年里,形态学算子在信号和图像处理系统中变得日益普遍。数学形态学最初用于二值图像。对于二值图像,数学形态学的基本概念和分析工具可在集合论和积分几何…I中发现。腐蚀和膨胀是其中两种最基本的算子它们的特点是用所谓的结构元素子集探测图像的内在结构,Matheron通过证明任何递增的算子可以用腐烛(膨胀)的交集(并集)表示HI,已经得到形态学算子的普遍存在性。在经典数学形态学中,图像探测应用中结构元素在大小和性状上保持不变,因此,其算子具有位移不变性。现在经典数学形态学主要有以下两个发展方向:①数学形态学与其它相关理论和方法相互渗透与融合,使数学形态学出现许多新的分支,例如顺序形态学,模糊形态学,形态神经网络和软数学形态学等;②随着应用需求的发展和理论研究的深入,算子的位移不变性约束显得非常荀刻,不能适应图像处理的需要。其实,每次结构元素选择的突破,都标识着数学形态学的一个重要发展。在参考文献[14]中,车辆交通控制摄像头得到的图像,在图像下面离相机比较近的车辆比在图像上面离相机比较远的车辆大。此时结构元素的大小应在图像的垂直方向上线性变化。这个例子直接促进了 SV数学形态学研究的开始。
………
第二章数学形态学理论框架
2.1预备知识
数学形态学作为一种图像处理方法,起源于集合论,主要基于集合理论以及晶格理论其本质是一种理论结构及其严密的数学方法,通过集合中的概念量化并表示图像的几何结构。数学形态学这门学科的兴起,推动了现代图像处理技术的快速发展,而且作为新出现的图像处理技术和理论,已经慢慢成为被图像处理研究领域专家极为看重的一个研究课题,现在它已经在一些领域取得了非常成功的应用,例如,医学图像处理、工业检测、计算机文字识别等丨气数学形态学方法最重要的就是选择一个合适的探针一一具有一定大小、形状、方向的结构元素,而对图像的处理方法是:令该探针在图像上有规律的移动,并与图像中对象相互作用,获取各对象之间的关系,最终有效地提取图像的形态学结构。有时为了处理那些结构复杂的图像,可能用到结构元素序列,以得到图像处理的最佳效果。
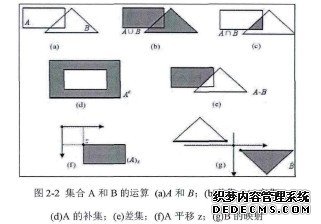
………
2.2经典数学形态学概述
二值图像处理是数学形态学理论最早期的应用,是灰度图像的特例,其每个像素不是黑就是白,灰度值为0或者1。一般把背景点像素取值为0,对应景物点像素取值为1。形态学膨胀、形态学腐蚀是数学形态学理论中最基本的算子,通过组合或者级联可以构造任意其它形态学算子。腐蚀、膨胀、开启运算和闭合运算这四个重要算子是数学形态学变换的基础。图2-4为膨胀过程的示意图,可以看出经过膨胀算子操作的图像中对象明显扩大了,使原图像更加饱满,起到了向外扩张、填补空洞的效果。公式(2.7)不是膨胀算子的唯一定义,不同的文献对膨胀有不同的定义。定义公式(2.7)把结构元素B当做卷积模板,对称映射后,使其在图像A上的连续平移,这个过程可以近似看成卷积的过程。
………
第三章SV数学形态学........ 29
3.1 二值图像的SV数学形态学........29
3.2灰度图像SV数学形态学........ 35
3.3 SVMM边缘检测算子........ 38
3.4本章小结 ........42
第四章医学图像处理........ 45
4.1医学图像处理的意义和方法........45
4.2计算机技术在医学图像处理中的应用........48
4.2.1在CT和MRI中的应用........ 48
4.2.2在显微镜图像中的应用........ 50
4.3本章小结........ 55
第五章SV细胞图像边缘检测........ 57
5.1基于微分算子的细胞边缘检测........ 57
5.2基于多元形态学细胞边缘检测........ 60
5.3基于SV形态学细胞边缘检测........ 62
5.4本章小结........64
第五章SV细胞图像边缘检测
5.1基于微分算子细胞边缘检测
基于微分算子边缘检测算法,首先求解原始数字图像中的每一像素点的微分向量,同时构造微分算子;然后对图像进行平滑处理,并利用模板、门限等方法获取边缘像素点。常用的微分算子有:Roberts、Sobel、Prewitt、Kirsch和Canny等一阶微分算子;Log和零交叉算子等二阶微分算子【67】。Roberts算子是大小为2X2的算子,根据图像灰度值的局部差分来计算边缘,它有一个显著的缺点:不对原始图像进行去噪处理,使得差分算子对噪声很敏感,所以对含噪图像进行边缘检测的效果很差。Sobel和Prewitt算子是大小为3X3的算子,通过算子模板与原始图像的卷积操作求解像素点梯度值,与Roberts算子相比,这两种算子尺寸稍大些,但对噪声的敏感度有一定降低,边缘检测效果也比较突出,然而对高浓度噪声仍然无能为力。Kirsch算子是一种具有方向特性的模板算子。相对于以上三种算子,Kirsch梯度判断更为准确,边缘检测更加精确,但其计算量却是最大的,同时仍不具备噪声抑制能力。这些都是典型的一阶微分算子,在边缘检测算法研究初期得到了广泛的认可和应用。
……..
结论
本文对数学形态学框架进行了系统的概述,深入研究了 SV数学形态学理论,并且提出了一种基于SV数学形态学的二值图像边缘检测算法。将它与SV数学形态学其它相关算法相结合,应用于医学图像处理中,得到了很好的处理效果,证实了 SV数学形态学在图像处理,进而在医学图像处理应用中的适用性。但是基于SV数学形态学算法的复杂性和多变性,还需要进一步的发现和研究。数学形态学是一种非常有用的图像处理工具,而且现在应用也非常广泛。SV数学形态学是其中的一个分支,由于它可对图像中结构很好的适用性,所以现在是一个重要的研究课题,而且国内外对这方面的研究相对较少,特别是国内。本文结合传统数学形态学的概念,性质以及基本算子,对SV数学形态的这些内容进行了研究。结合医学图像的特点,将其应用在细胞图像边缘检测上面,进一步阐述了 SV数学形态学在理论上的可行性和优越性。而对医学图像处理领域的研究来说,本文工作在一定程度上为其添加了新内容和方法,希望可以产生更加深远的影响。
…………
参考文献(略)
