本文是一篇医学论文,本文通过控制其他参数数值不变,只改变某一个重要影响参数的数值来预测乙肝感染人数的变化趋势,观察哪一个参数的影响最大,从而有针对性地提出有效措施。
第1章 绪论
1.1研究背景及意义
乙型病毒性肝炎(Hepatitis B,简称乙肝)是能够导致肝功能严重受损的一种病毒性传染病[1]。它具有传播范围广、感染人数多和危害程度高等特点[2]。乙肝分为急性乙肝和慢性乙肝,对于感染急性乙肝的成人,在不治疗的情况下有90%的概率自愈,但慢性乙肝不能自愈[3]。乙肝的危害程度和包括艾滋病、结核病和疟疾在内的世界三大传染病相比有过之而无不及[4]。WHO在2016年提出目标:到2030年我们需要解除病毒性肝炎对公共健康的威胁。以2015年为基础,病毒性肝炎感染率到2030年至少要下降90%,死亡率需要下降65%[5~6]。2019年全球有110万人因为感染乙肝而死亡,这与2015年相比仅仅只减少了30万人。所以,提高乙肝的治病比例和诊断比例还有待进一步的努力,降低死亡率目前仍然是一个巨大的挑战。
中国处于乙肝中度流行区。中国在1970年前,患有乙肝的人数是4000万左右,从1970年到1992年20年时间内,乙肝病毒携带者增长到1.2亿人,从此被称为乙肝大国。直到2020年10月28日,国新办举行了一场发布会,并讲到中国肺结核报告的发病率在2015年时是63.4/10万,在2019年的时候下降到了55.6/10万,5岁以下儿童乙型肝炎病毒(HBV)感染率降至1%以下,自此我国被誉为发展中国家典范。虽然我国不再是乙肝大国,但是在中国人十大死亡原因排名中,肝癌位列第六,肝癌中,我国有80%都与乙肝有关,所以乙肝对人们的健康仍然具有威胁。目前我国感染乙肝的人数占到全球的1/3左右。2019年我国乙肝报告的发病率为71.77/10万人,死亡率为0.032/10万人。其实整体看来,与前几年相比而言,我国乙肝发病率以及死亡率均为增长趋势,形势依然十分严峻。在我国,西部地区是我国的高发地区,乙肝发病率高达8.92%。广西地区扶绥县是我国原发性的肝癌高发地区[7],其肝癌死亡的比例达到了全国平均水平的2倍,高达55.62/10万。因此本文选择广西壮族自治区作为我们研究的地区。
1.2乙肝预测模型的研究进展
传染病按照其预测的方法分类,可以被分为定性预测和定量预测。定性预测主要有比数图法、控制图法等;定量预测主要有动力学模型预测法、时间序列模型预测法等[11~12]。不同类型的传染病适合用不同的预测方法。由于乙肝的高传染率,乙肝已经成为一个全球性的健康问题,大量的预测方法被用来预测HBV的流行规律和发展趋势。
许多学者利用统计学的方法预测传染病发病数。马金宇等人[13]针对2005年至2020年的宁夏乙肝月发病人数建立ARIMA模型,并预测2021年宁夏乙肝的发病人数,研究结果显示,ARIMA模型对宁夏的乙肝月发病人数具有良好的分析和预测效果。周瑜等人[14]针对2009年至2019年泸州市的乙肝发病人数,分别从地区、时间、人群、职业的分布情况进行分析,并建立了ARIMA模型,利用此模型对2020年的泸州市月发病人数进行预测,预测结果显示,2020年1-6月的发病率处于较低水平,7-12月的发病率则处于较高水平。郝启迪等人[15]通过建立BP神经网络模型与ARIMA模型,对2009年至2019年的新疆生产建设兵团乙肝发病数据进行研究,研究结果表明,BP神经网络的预测效果比ARIMA模型的效果要好一点,但基本差不多。李可馨[16]针对2005至2018年的我国乙肝发病人数,分别建立ARIMA模型、支持向量机模型和灰色预测模型,通过比较这三个模型的预测效果得到,支持向量机的预测效果是这三个模型中最好的,并利用预测效果最好的模型对乙肝月发病人数进行了预测,预测结果显示,我国乙肝在2月和3月份增长比较剧烈。谭姣等人[17]对2004年1月至2012年6月陕西省某市乙肝发病率构建ARIMA模型,模型预测效果良好。李滨等人[18]针对辽阳市2004年至2012年的乙肝发病率,分别建立了传统预测模型和残差修正模型,发现后者的预测效果更为理想。
第2章 相关理论
2.1机器学习模型介绍
2.1.1差分整合移动平均自回归(ARIMA)模型
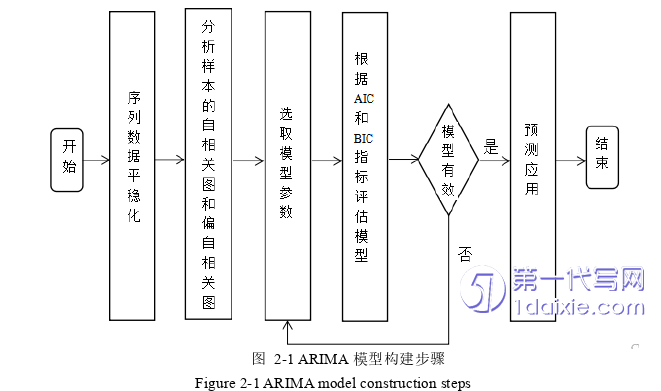
George Box和Gwilym Jenkins提出自回归移动平均模型(ARMA),适合用来预测随机时间序列。该模型的应用要求时间序列满足平稳性,但是现实中的时间序列大部分都是非平稳的,所以为了能够处理非平稳的时间序列,则需要用到自回归求和移动平均模型(Autoregressive integrated moving average,ARIMA)。其本质是将非平稳序列通过处理变成平稳序列之后再应用ARMA模型,具有两种形势,分别为季节性(,,)(,,)sARIMA p d q P D Q模型和非季节性ARIMA(p,d,q)模型,其中p,q为自回归和移动平均次数;d,D为使序列平稳化的差分次数和季节差分次数;P,Q为季节自回归和移动平均阶数,s为周期。使用ARIMA模型主要分为6个步骤,该步骤图如图 2-1所示。
2.2动力学模型介绍
Kermack与McK endrick在1927年创立了“仓室”模型,一直以来被广泛应用于传染病的研究中,SIR模型与SIS模型是他们提出的两个经典的基本模型[38],大量传染病数学模型的建立与分析都是基于此经典模型,本文也是以此经典模型为基础建立的乙肝传播动力学模型。下面我们对这两个基本模型进行介绍。
2.2.1SIR模型
一般来说,染病治愈后具有免疫能力的疾病适合用SIR模型描述。SIR模型将人群分为三种:
易感者(Susceptibles)类:记为S,表示没有被感染,但是有被感染可能的人群,S(t )表示t时刻未被感染,但是有被感染风险的人数。
染病者(Infectives)类:记为I,表示被感染并且具有传染能力的人群,I(t )表示t时刻已经被感染并且具有传染能力的人数。
移除者(Removed)类:记为R,表示已经被治愈、死亡或者被隔离的人群,R(t )表示t时刻去世、隔离或者获得免疫能力的人数。 设t时刻总人口为N(t ),则有N(t)=S(t )+I(t)+R(t )。SIR模型的建立基于以下三个假设:
(1)假设所有人都处于一个封闭环境中,不考虑人口的出生、死亡、流动等因素,此时这个封闭环境中的总人口数始终是一个常数,即S(t )+I(t)+R(t )≡K。
(2)假设患病者只要与易感者有接触就必定会被感染。假设t时刻单位时间内,一个患病者能传染的易感者人数与易感者的总人数之间成正比关系,比例系数为β,从而在t时刻单位时间内易感者被所有染病者传染的人数为βS(t)I(t )。
(3)假设t时刻单位时间内从染病者移出的人数与染病人数成正比,比例系数为γ,因此单位时间内移出者的数量为γI(t )。
第3章 基于机器学习的广西乙肝传播模型预测...........................13
3.1数据分析与数据预处理..................................13
3.1.1数据分析.........................................13
3.1.2数据预处理...........................14
第4章 基于动力学模型的广西乙肝传播预测..............................23
4.1动力学模型.............................................23
4.1.1乙肝动力学模型....................................23
4.1.2基本再生数............................................24
第5章 机器学习方法与动力学模型在传染病传播预测上的对比研究........33
第5章 机器学习方法与动力学模型在传染病传播预测上的对比研究
为了得到机器学习方法与动力学模型在乙肝预测上的效果对比结果,我们分别利用机器学习方法和动力学模型预测2018年1月至2019年10月的广西乙肝月发病人数,将预测结果与实际感染人数进行对比。由3.2节得到ARIMA模型、LSTM模型、ARIMA—LSTM并联组合预测模型以及ARIMA—LSTM串联组合预测模型在2018年1月至2019年10月乙肝月发病人数预测中,ARIMA—LSTM并联组合预测模型的预测效果最佳,于是我们在比较机器学习方法和动力学模型在乙肝传染病传播预测时,选择ARIMA—LSTM并联组合预测模型与乙肝动力学模型进行比较。ARIMA—LSTM并联组合预测模型关于2018年1月至2019年10月广西乙肝月发病人数的预测结果已经在3.2节中得到了,接下来需要利用动力学模型进行预测。
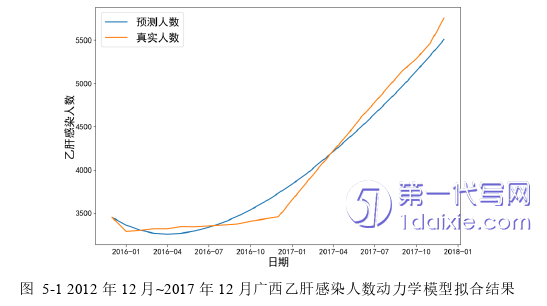
利用2015年12月至2017年12月的发病人数进行动力学模型拟合,得到拟合结果如图 5-1所示,对应的模型评价指标MAPE=2.1%、MAE=77.24、RMSE=95.89,拟合效果良好。于是我们可以利用2012年12月至2017年12月拟合得到的动力学模型来预测2018年1月至2019年10月的乙肝月发病人数,并将其与真实感染人数进行比较。ARIMA—LSTM并联组合预测模型和动力学模型对于2018年1月至2019年10月的广西乙肝月发病人数预测结果如图 5-2所示。图 5-2中垂直的的虚线将整个预测时间段分成2018年1月至2018年6月和2018年6月至2019年10月两个时间段,2018年1月至2018年6月的预测结果视为两个模型关于乙肝感染人数的短期预测,2018年6月至2019年10月的预测结果视为中长期预测。从图 5-2中可以明显的看出ARIMA—LSTM并联组合预测模型相比于动力学模型预测效果要好很多,并且不管是短期预测还是中长期预测,ARIMA—LSTM并联组合预测模型的预测效果都要比动力学模型的预测效果好。
第6章 总结
本文针对2004年1月至2019年10月的广西地区乙型肝炎月发病人数分别进行机器学习和动力学模型预测分析,比较了两者在传染病预测方面的优势与不足。主要内容总结如下:
在传染病预测领域,ARIMA模型的应用较为广泛并且预测精度较高,能够较好地拟合时间序列数据的线性趋势。同时,LSTM模型能够很好地拟合时间序列数据的非线性趋势。因此,为了提高对乙肝感染人数的预测精度,并利用精度较好的机器学习模型与动力学模型进行对比,考虑将两者结合,建立ARIMA—LSTM并联组合预测模型和ARIMA—LSTM串联组合预测模型。利用这四个模型分别对2018年1月至2019年10月的广西乙肝月感染人数进行预测,挑选出预测精度较高的模型。试验结果显示四个模型中ARIMA—LSTM并联组合预测模型的精度最高,并且拟合效果最理想。
考虑到乙肝病毒感染者后期才会具有传染性,在文献[39]的基础上将潜伏者这一仓室去除,建立新的乙肝病毒传播动力学模型并利用下一代矩阵法计算模型的基本再生数。针对2004年1月至2019年10月广西地区乙型肝炎的月发病人数,利用建立的动力学模型对该数据进行分析研究。
为了了解防控策略与模型中参数的关系以及提出有效控制乙肝感染人数的策略,我们分析了防控策略对参数的影响。结果显示,防控策略会通过影响某些特定参数来改变疾病的流行趋势,从而达到防治的目的。
参考文献(略)
