本文是一篇计算机论文,笔者认为现有的多层网络社区发现算法大多用于检测非重叠的社区结构,本文提出的两种算法无法应用于检测多层网络的重叠社区,因此未来考虑研究用于检测多层网络重叠社区的算法。
1绪论
1.1研究背景及意义
现实世界中的很多复杂系统都可以表示为复杂网络,例如社会学中的人际关系网、生命科学中的蛋白质交互网、因特网和万维网、城市交通系统等,社团结构是复杂网络的一个重要特征,即同一个社区内节点之间连接紧密而不同社区间节点之间连接稀疏[1]。例如,社交网络的社区代表具有相似特征的人群、蛋白质交互网络中社区代表具有相似功能的生物组织模块、万维网中不同的社区代表不同的功能的网页。社区发现是复杂网络分析挖掘中的重要任务之一,对于网络拓扑结构分析、功能分析和行为预测具有重要意义,已在社会学、生物信息学、交通系统等领域得到了广泛应用[2-4]。例如,在社交网络中,社区发现有助于分析用户的社会行为和信息的传播路径以及预测网络的变化趋势[5];在生物网络中,社区发现有助于分析属于共同功能模块的蛋白质之间的相互作用[6];在交通网络中,社区发现可以通过对城市道路网络划分为多个支线网络来实现对城市交通系统的区域控制,从而缓解城市道路堵塞问题[7]。
针对不同的应用领域,研究者近年来已经开展了广泛研究,并提出了系列社区发现算法,主要包括:基于划分的方法[8]、基于模块度的方法[9-10]、基于谱的方法[11]、基于动力学的方法[12]、基于标签传播的方法[13]等。已有算法大多适用于单层网络,然而现实世界中由多种类型节点及其连边关系组成的多层网络更为普遍存在[14]。例如,社交网络中的个体之间可能存在不同类型的社交关系,如好友、关注、评论、转发等;在生物网络中,对于某些生物体来说,对完整的蛋白质与蛋白质相互作用涉及数千种蛋白质分子之间多种不同的相互作用模式;在航空运输系统中,通过直飞航班对机场之间的连接建模,不同的商业航空公司可以被视为机场之间的不同连接模式。与单层网络相比,多层网络结构具有更加丰富的拓扑信息,有助于更为准确地探测网络中蕴含的社区结构[14]。
1.2国内外研究现状
近年来,一些学者针对多层网络的社区发现问题已经开展了有益探索,提出了相应的算法[15-16]。根据方法的实现机制可以将现有的多层网络社区发现算法大致分为两类,即基于聚合的方法和基于扩展的方法[15]。
(1)基于聚合的方法
为了降低社区检测的难度,相关研究基于多层网络的聚合结构进行社区发现,具有实现简单、可扩展性强的特点。主要包括基于网络聚合和基于集成学习两类思路。
基于网络聚合的方法将一个多层网络压缩成单个网络,然后采用单层网络的社区发现算法对其进行社区检测。最简单的策略就是对邻接矩阵进行加权,其中2个节点之间的权值为它们在多层网络中相连的层数,但这种方法容易丢失网络的信息,且结果不稳定。Berlingerio等人[17]对上述简单的加权策略进行了修改进而提出了基于节点在多层网络中的共同邻居的数量而构造邻接矩阵的策略。这种策略不再考虑两个节点之间的直接联系,而是关注它们的邻居,共同邻居数越多则它们越有可能在同一个社区。Zhu等人[18]进一步考虑了每层网络的重要性,将单层网络之间的相关性与单层网络的重要性密切联系起来,若某一单层网络与其他的单层网络之间的相关性更大,则表明其重要性更强。同时利用两个节点之间是否存在路径来衡量节点相似度,然后结合两者构造一个统一矩阵,最后再利用单层网络社区发现算法得到最终的社区划分结果,该方法虽然同时考虑每层网络的重要性和节点相似度,但由于其在衡量节点相似度时需要使用一个参数来确定两个节点之间的路径长度,所以该方法存在时间复杂度高的问题。Pan等人[19]首先将多层网络聚合为一个单层网络,然后给定一个参数τ将聚合图中小于τ的边去除,最后利用单层社区发现算法得到社区划分结果,该算法实现简单,在一定程度上可以保留多层网络中的主要信息,但其忽略了每层网络的重要性,且多层网络的简单聚合容易造成社区划分结果不准确。该类方法在聚合过程中丢失了不同层网络结构的独特性,造成社区结果的不准确。
2社区发现算法
介绍2.1单层网络与多层网络
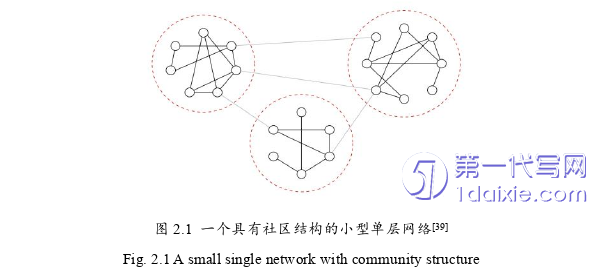
单层网络即一般的复杂网络,指由众多连接关系复杂的节点组成的网络。单层网络由于能够广泛的应用于各个领域对复杂系统进行建模和分析,受到了学者们的广泛研究,且随着研究的不断深入,学者们发现社团结构是复杂网络的一个重要特征,即同一个社区内节点之间连接紧密而不同社区间节点之间连接稀疏[1]。社区发现是分析各种复杂网络的一种最流行的研究方法,也是复杂网络分析中的重要任务之一。如图2.1所示为一个具有社区结构的小型单层网络,包含三个独立的社区,可以明显看出社区内节点之间的连边较多,而社区之间连边较少。
随着进一步的研究,学者们也意识到许多复杂网络本质上可由多层网络表示,例如,在一个社交网络中的个人可能与其他人存在多种互动(如关注、转发、回复、提及等)[40],而仅仅在单层网络上进行社区发现并不能更好的分析现实世界中的复杂网络结构。如图2.2中所示为一个多层网络AUCS数据集,其中每层网络节点相同,表示某大学研究部门的61名员工,各层网络分别表示他们之间的工作关系、午餐关系、Facebook关系、休闲时间关系和合作关系[41],单层网络社区发现算法并不足以探测该网络中所蕴藏的社区结构。
2.2单层网络社区发现算法介绍
经典的单层网络社区发现算法包括基于划分的方法[8],基于模块度的方法[9-10],基于谱分析的方法[11],基于标签传播的方法[13]等。本节对单层网络社区发现算法中几类方法进行简单介绍。
基于划分的方法。基于划分的社区发现算法的基本原理是首先找到社区间的所有连接,然后将它们全部删除,最后每个连通分支对应一个社区。其中,最经典的算法为Girvan和Newman提出的GN算法[43],该算法的核心思想是社区间的边介数大于社区内的边介数,该算法重复的计算边介数,并不断删除边介数最大的边,删除至网络中没有边时算法停止,这个过程可以通过一个自顶向下的层次聚类树来表示,最优划分可以通过模块度函数来进行判断。
基于模块度的方法。2004年,Girvan和Newman[44]定义了模块度函数Q用于定量的衡量网络的社区划分。Girvan和Newman提出了FN算法[9],该算法初始化时将每个节点都视作一个单独的社区,每次迭代合并使Q值增加最大的社区,当合并至仅有一个社区时算法结束,它的过程可以通过一个自底向上的层次聚类树来表示,最后Q值最大的社区划分作为最终结果。Blondel等人[10]提出了快速模块度优化方法,首先将每一个节点都表示为一个单独的社区,通过优化Q函数达到局部最优,再通过将每个社区视为超节点计算Q值,直到Q值不再变化结束算法。
3 基于两阶段集成的多层网络社区发现算法 ................... 11
3.1 引言 ................................... 11
3.2 基于两阶段集成的多层网络社区发现算法 ................................ 11
4 基于二部图集成的多层网络社区发现算法 ...................................... 25
4.1 引言 ................................... 25
4.2 基于二部图集成的多层网络社区发现算法 ................................ 25
5 总结与展望........................................ 33
4基于二部图集成的多层网络社区发现算法
4.1引言
多层网络中层与层之间由于包含的信息量不同而有着不同的重要性,而一些方法往往对不同层统一看待,另一方面基于集成学习的方法在对各层社区划分进行融合时往往忽略不同层社区之间存在异质性,且不同社区也有着不同的重要程度,从而导致难以获得准确的社区划分结果。另外,随着大数据时代的来临,如何从大规模多层网络挖掘有意义的知识成为一个亟待解决的问题,本文第三章提出的基于两阶段集成的多层网络社区发现算法能够有效融合不同基社区结构和社区划分之间的重要性,但存在计算效率低的问题,无法应用于较大规模的多层网络。
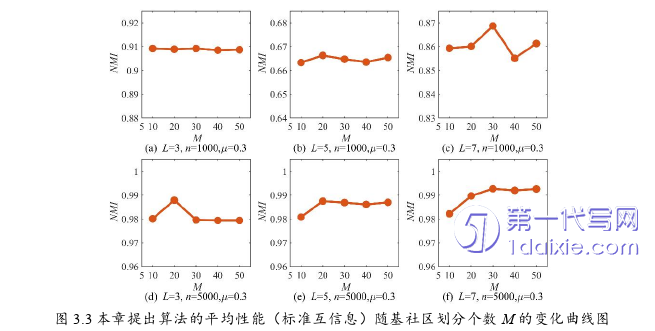
针对上述问题,本章提出了一种基于二部图的多层网络社区发现算法,旨在有效融合不同网络层的信息,提高社区发现结果的准确性和可解释性,提高算法计算效率。该方法首先计算各层网络的重要性,然后对基社区划分中的局部社区进行可靠性度量,并通过结合各层网络的重要性衡量各个社区的重要性,将多层网络构造为二部图,最后通过二部图社区发现算法得到最终社区划分结果。在60个人工合成网络和8个真实网络上的实验结果表明,本章提出的算法相较于对比算法具有一定的优势。
5总结与展望
复杂网络作为具有多种前瞻性应用的跨学科研究,越来越受到科学界的关注。受社会网络、生物网络和交通网络等现实世界场景的启发,广泛的研究已经致力于从复杂网络中提取有意义的知识。而随着进一步的研究,学者们也意识到许多复杂系统本质上可由多层网络表示,虽然每层网络表示不同的关系模式,但它们之间存在潜在的联系,因此发掘多层网络的社区结构具有重要的意义。基于集成学习的多层网络社区发现算法由于其实现机制简单、可扩展性强等特点被广泛关注,但是,该类方法存在许多不足,例如容易忽略不同层社区之间的异质性,在融合过程中易忽略不同的基社区结构和社区划分之间的重要性,易丢失信息,结果不稳定,算法运行效率低等一系列问题。
本课题提出了两种多层网络社区发现算法,有效的解决了基于集成学习的多层网络社区发现算法易忽略不同层社区之间的异质性,在融合过程中易忽略不同的基社区结构和社区划分之间的重要性,运行效率低等问题。本文主要研究内容如下:
(1)提出了基于两阶段集成的多层网络社区发现算法。首先,第一阶段在各层进行局部集成时结合了其他层的最优社区划分信息,有效利用了不同网络层社区结构的相关性;其次,第二阶段中基于其他网络层的社区结构信息对各层融合得到的社区划分及社区结构的重要性进行评价加权,再进行全局加权集成,综合考虑了各层局部社区划分结果对集成的影响。最后,通过在人工生成多层网络和真实多层网络上进行实验分析,对提出算法的有效性和鲁棒性进行了验证。实验结果表明,所提出的算法在人工合成网络和真实网络上具有一定的优势,相比对比算法更加准确有效。
(2)提出了一种基于二部图集成的多层网络社区发现算法,有效地提高了算法的计算效率以应对大规模多层网络社区发现所面临的挑战。该算法计算多层网络中各层网络的重要性,利用信息熵计算各个社区结构的可靠性,通过将二者结合得到各个社区的最终权重并构造二部图,采用二部图社区发现算法得到最终社区划分结果。实验结果表明,本章提出算法在人造数据集和真实数据集上相比对比算法具有一定的优势。
参考文献(略)
