本文是一篇计算机论文,本研究提出了MR-FKSVM算法。为了解决节点负载不均衡的问题,提出了基于K-means的数据划分策略DSK,利用并行K-means均匀划分数据集,平衡节点负载;为了解决冗余数据过多的问题,提出了基于fisher投影的FS-FPD策略,利用三角向量判定法则识别冗余数据;
第一章 绪论
1.1 研究背景与意义
随着信息时代的到来,各行各业产生的数据信息迅速增长,深入分析和挖掘海量数据中的有效信息对于促进经济持续增长、提高企业竞争力发挥重要作用[1]。大数据被誉为“未来的新石油”,是21世纪信息技术的强劲引擎,大数据具有模态多、规模大、价值大密度低、时效性高和精确性等特征[2-3]。在此背景下,如何利用现有技术处理大规模数据,是当前迫切需要解决的问题,其中数据挖掘是大数据分析技术的基础,是分析、处理海量数据的重要手段。
数据挖掘也叫数据库知识发现[4],它将处理海量数据的复杂算法与传统的数据分析方法相结合,主要通过统计学、机器学习以及模式识别等方法实现。数据挖掘的任务主要包括分类分析[5]、关联分析[6]、聚类分析[7]等。其中,SVM作为机器学习中经典的分类算法[8],它通过训练带标签的数据得到分类模型,再使用模型预测数据标签,由于其具有较高的准确度和防止过拟合能力[9],目前已被广泛应用于图像识别[10]、文本分类[11]、生物医学[12]、人脸识别[13]、股票预测[14]等多个领域。然而,随着大数据时代的来临,内存消耗大以及训练时间长成为限制SVM发展的关键因素[15-16],这严重制约了SVM算法在大数据环境下的应用。为了突破性能瓶颈,研究人员设计出了并行SVM算法,目前已知的SVM并行算法主要有:级联式SVM[17-20]、近似算法[21-23]、并行分解算法[24-27]等,这些并行实现在模型准确率、训练时间、内存需求、可拓展性等方面各有优缺点。级联式SVM虽然避免了节点间的通信开销,但是降低了最终模型的准确率;近似算法使用内点法求解QP问题得到最终SVM模型,并使用近似矩阵分解来减小内存占用,然而矩阵维数参数的设置不好把控,无法兼顾训练时间和模型准确率;
1.2 国内外研究现状
近年来,随着MapReduce并行计算模型的快速发展,以及Hadoop、Spark[28-30]等分布式并行计算框架的广泛应用,为SVM算法的并行化研究提供有力的技术支撑[31]。B等人[32]首次将MapReduce模型应用于机器学习领域,并给出了线性SVM的MapReduce算法。Kun等人[33]将数据集均匀的划分成若干个数据子集,对每个子集进行SVM训练,把得到的SVM模型合并为最终分类器。Alham等人[34]基于Hadoop分布式平台和Bagging思想提出了并行集成SVM算法,该算法在Hadoop平台上搭建MapReduce计算模型并行训练SVM,有效的减小了SVM的训练时间,并且保证了算法的分类准确率。然而,随着样本数据的增加,算法的运行时间也会迅速增长,且对于数据集的切分数量和准确率之间的平衡难以把握。为了确保并行SVM算法的分类准确率不会损失太多,Graf等人[17]提出了级联式SVM模型,该模型将数据集分解成多个不重叠的子集,在各子集上分层训练SVM模型,得到的支持向量集两两合并之后发送到下一层进行训练,直到只剩下一组支持向量集。Hsieh等人[20]在Graf的基础上提出了DC-SVM,该算法使用K-means对数据进行聚类划分来代替级联式SVM的随机划分,根据聚类结果在各个类别的数据上求解SVM,并将所有变量发送到下一层作为下一层的输入。You等人[19]提出的CA-SVM算法对DC-SVM算法做了进一步的简化,在算法训练到一定层数得到多个SVM模型时终止训练,分类时选取距离样本最近的SVM模型进行分类,该算法的训练时间更短、可扩展性更强,但是存在分类准确率的损失。为了提高训练效率的同时保证算法的分类准确率,Sun等人[64]提出了基于MapReduce的MR-TSVM算法,该算法在map任务中动态筛选支持向量,并将各map节点的训练结果合并后发送到reduce迭代训练SVM。此基础上,为了提高并行SVM对大型数据集的并行处理能力,Jadhav等人[35]提出了基于MapReduce框架的级联式并行SVM(MR-PSVM),MR-PSVM算法将级联式SVM迁移到MapReduce框架上,使用map函数分层训练SVM,在reduce函数中,将SVM训练得到的子集两两合并,输入下一层,在最后一层得到全局SVM模型。该算法充分利用MapReduce框架的并行优势,有效的提高了SVM的并行化效率。
第二章 相关理论概述
2.1 MapReduce计算模型
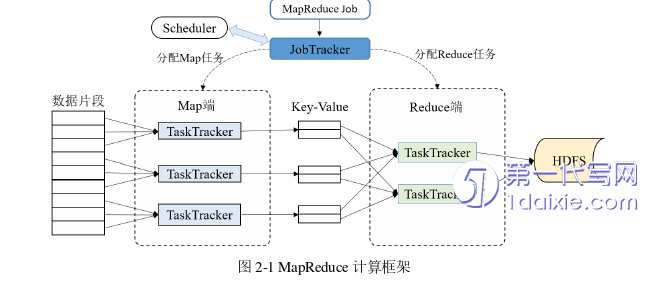
MapReduce框架是由Google公司开发的一种能够处理海量数据的高性能分布式编程框架[26], Google文件系统为MapReduce分布式计算提供了高效可靠的数据管理。MapReduce由连个主要的并行阶段组成,map阶段和reduce阶段。Map阶段使用用户自定义的map函数对数据集中的每个元素进行计算。map函数将key-value对作为参数输入,并输出key-value中间值。Reduce阶段使用用户自定义的reduce函数合并具有相同key的value,而shuffle阶段则会集合所有具有相同key的key-value对。MapReduce模型不需要用户考虑并行化的具体细节,用户只需要专注于数据的处理函数即可。MapReduce框架的架构如图2-1所示:
2.2 支持向量机理论
支持向量机是由Cortes和Vapnik[8]于1995年提出的基于统计学习理论[48]的一种分类技术,具有较强的泛化能力、完善的理论知识和获取全局最优解的能力[49],并在许多实际应用(手写数字识别、文本分类等)中展示了大有可为的实际效用。SVM分类的过程就是寻找最大间隔超平面的过程,以最优超平面最大限度地将两个类别的数据分隔开来[50],因此SVM也经常被称为最大边缘分类器,距离超平面较近的向量称为支持向量[51]。接下来我们将详细介绍SVM算法处理线性和非线性问题的基本思想和原理,并阐述级联式SVM的执行流程。
2.2.1 线性支持向量机
线性的主要思想是在有限的空间内寻找一个到能够将正负样本分隔开来的超平面,并且在一定容错下尽可能的使间隔更大。简而言之,就是使用SVM进行线性分类要满足两个条件:其一是边缘超平面能够正确的划分两类样本点,并且不同类别的样本分别位于超平面的两侧;其二是正类样本组成的支持向量到负类支持向量组成的决策平面的距离要最大化,反之亦然。只有满足了上面这两个条件,SVM所求得的目标函数才是问题的最优解,由此获得的分类模型才能保证较高的分类精度。
第三章 基于Relief 和BFO 的并行 SVM 算法 .................... 17
3.1 噪音数据过滤 ............................. 17
3.2 并行参数选取 ................................. 19
3.3 并行SVM模型构建 .............................. 24
第四章 基于fisher 投影和聚类的并行 SVM 算法 .................... 40
4.1 数据划分 ............................ 40
4.2 冗余数据删减 ....................................... 42
4.3 并行SVM模型构建 ..................................... 45
第五章 总结与展望 .................................... 54
5.1 总结 ...................................... 54
5.2 展望 ................................................ 55
第四章 基于fisher投影和聚类的并行SVM算法
4.1 数据划分
在分布式并行计算过程中,算法的运行时间由负载最大的节点决定,因此,平衡节点负载对于降低并行SVM算法的时间复杂度至关重要。本文提出了基于K-means的数据划分策略DSK,将数据集均匀地划分到各个节点,降低算法的时间复杂度。DSK策略主要由以下两个步骤组成:(1)并行K-means聚类:分别将正负类并行聚类成相同数目的簇,每个正类簇具有相同数量的正类样本,负类簇具有相同数量的负类样本;(2)均匀数据划分:为每个节点分配簇中心距离最接近的一个正类簇和一个负类簇,正负类在每个节点上的比例相近。用DSK策略进行数据划分的具体过程如下:
(1) 并行K-means:在相关算法介绍中我们已经了解了K-means算法的执行步骤,假设用户设置的处理器节点数为n,对于并行K-means聚类我们首先将正负类原始数据集分别均分到各个节点上,即正类分成n份,每个节点分到的样本数e =N/n(N为原始数据集规模),负类同上;接着,初始化2n个初始簇中心并告知所有进程,并行计算每个正类样本到n个正类簇中心的距离,每个负类样本到n个负类簇中心的距离,每个样本都选择距离最近的中心点作为簇中心;其次,在簇中心更新阶段,各处理器节点计算各个簇的局部的样本和;最后,在经过threshold次迭代运算之后,样本所属簇中心不再发生改变。
并行K-means算法的伪代码如算法4.1所示:

第五章 总结与展望
5.1 总结
大数据环境下收集到的数据,其数量和维度不断增加,要利用有限的计算资源挖掘出数据中隐藏的有价值的信息,并且解决大规模数据集训练时存在的计算开销大、时间复杂度高等问题,就需要设计出高效的、可拓展的方法,算法并行化就是这样一种方法。本文围绕如何降低大数据环境下并行SVM算法存在的噪音数据敏感、参数选取困难、并行化效率低等问题,提出了RBFO-PSVM算法,同时,为了解决并行SVM算法训练时存在的节点负载不均衡、冗余数据过多、计算开销大等问题,提出了MR-FKSVM算法,并通过仿真实验验证了这两种算法的可行性和有效性。本文的主要工作总结如下:
(1) 提出RBFO-PSVM算法。首先,为了减少噪音数据对SVM训练的干扰,结合Relief和互信息的特性提出了MI-Relief策略,该策略通过计算特征与类别的相关性,特征与特征之间的冗余性来判定特征是否为噪音数据,有效的识别并删除了数据集中的噪音数据;其次,为了解决SVM参数选取困难的问题,提出了基于BFO和MapReduce的MR-HBFO算法并行选取最优参数;最后,为了提高并行SVM的并行化效率,提出核聚类策略KCS减小数据集规模,并提出改进CSVM反馈机制的交叉融合CFCPSVM模型,基于MapReduce框架构建实现模型,有效的提高了并行SVM的运行效率。实验表明,RBFO-PSVM算法不仅具有良好的分类效果,而且在处理大型数据集时也有不错的表现。
(2) 提出了MR-FKSVM算法。为了解决节点负载不均衡的问题,提出了基于K-means的数据划分策略DSK,利用并行K-means均匀划分数据集,平衡节点负载;为了解决冗余数据过多的问题,提出了基于fisher投影的FS-FPD策略,利用三角向量判定法则识别冗余数据;为了减小并行SVM的计算开销,提出了自适应停机策略ASS-JC,通过比较上下层训练结果来判断当前层的运行效率,去除低效层,有效节省了计算开销。此外,为验证MR-FKSVM算法的性能,在character、crop、PAMAP2、microblogPCU四个数据集上比较、分析MR-FKSVM算法与其他三个并行SVM算法的运行时间和分类效果,从实验结果可知,MR-FKSVM算法展现出了较为出色的性能。
参考文献(略)
