本文是一篇计算机论文,本文主要研究了PSO算法在陶瓷配方问题上的应用求解。首先介绍了粒子群优化算法的基本原理、诞生及发展过程,并详细阐述了粒子群算法中几个重要参数:惯性权重w,学习因子c1,c2在算法寻优中的性能影响。
第一章绪论
1.1研究背景及意义
陶瓷是一种古老的手工艺品,可以追溯到公元前10000年左右的新石器时代。它是指用黏土等天然材料制作的陶器、瓷器和瓦器等制品。中国是世界上最早发明和生产陶瓷的国家之一,中国的陶瓷历史可以追溯到公元前16000年左右的新石器时代,距今已经有数千年的历史。中国的陶瓷在世界上享有很高的声誉,因为其质量、造型、装饰和技术一直处于世界领先地位。在中国的历史上,陶瓷的发展经历了几个时期。最早的时期是原始陶器时期,其次是新石器时期和青铜时期,然后是汉朝、唐朝和宋朝时期。在这些时期中,陶瓷的制作技术不断改进和创新,从最初的手工制作逐渐转向机器生产。现代陶瓷制造技术的发展使得陶瓷产品的种类越来越多,应用范围也越来越广泛,例如餐具、建筑材料、电子器件、医疗器械、航空航天等等领域。现代陶瓷的制作工艺也变得越来越自动化和精细化。
陶瓷产品生产原料大部分是来自天然的矿物岩石,这些原料种类繁多且分布地域化明显,而在陶瓷产品生产过程中,最重要的就是陶瓷配方的设计。陶瓷配方是指根据已有的陶瓷制品的坯、釉料进行化学组成分析得到其化学成分组成及百分含量比,陶瓷配方设计是指根据已有的陶瓷配方,选取所需的生产原料并决定其各种原料的百分含量比。陶瓷配方设计过去主要依靠无数从业人员在专业理论的指导下,通过大量的试验生产和分析试验品化学组成与物理性能,在考虑成本、利润、生产难度等多方面因素后,最终得到的设计方法。这种高度依赖从业人员的专业经验和知识,且具有不确定性的配方设计方法,不利于现代陶瓷行业的现代化、智能化发展需求。因此,需要采用更系统化、智能化的方法来对配方设计进行优化。
1.2 PSO算法国内外研究现状
粒子群优化算法(Particle Swarm Optimization,PSO)是一种常用的优化算法,用于求解非线性、非凸、多峰、高维等问题。它模拟了鸟群捕食的行为,通过不断调整粒子的位置和速度来寻找最优解。
PSO算法自提出以来,得到了广泛的应用和研究,PSO算法最早由Kennedy和Eberhart于1995年提出,随着学界对其研究的逐渐深入,PSO算法逐渐改进和完善,并应用于诸多优化问题。目前针对粒子群算法的改进与研究主要集中在以下几个方面:(1)算法参数的改进研究(2)算法的收敛性分析(3)PSO算法与其他算法的混合改进(4)算法的拓扑结构研究。
在算法和其他算法混合改进的方面,不少学者通过将粒子群优化算法与其他优化算法相结合,或者吸收其他优化算法的思想进行改进,提出了诸多混合算法。例如,文献[11]结合了模拟退火思想与杂交思想,将其引入具有高斯变异的粒子群优化算法中,增强了算法的局部跳出能力。周蓉等[12]结合灰狼算法提出了基于灰狼优化的反向学习粒子群算法,提升了算法的收敛精度。此外,PSO-SA[13-14]、PSO-GA[15-16]、PSO-ACO[17]、PSO-DE[18-19]、PSO-TS[20-21]等诸多混合算法纷纷提出,并用于解决理论优化与实际工程问题。
第二章相关知识
2.1粒子群优化算法
2.1.1粒子群算法基本原理
大自然中鸟类在觅食过程中,往往是群体行动,在鸟类种群中,每只鸟的飞行速度与飞行方向都各不相同,然而在发现食物之后,飞行速度与方向各不相同的鸟类却最后总能汇聚到食物最多的地方,在这种觅食过程中,鸟类个体由于飞行速度方向与视力等个体限制,其觅食范围是有限的,可能无法寻找到食物位置,然而,鸟类种群可以通过鸟类之间的互相交流,获取彼此之间觅食的经验,从而使整个种群能够快速的寻找到食物位置。这种个体间遵循极其简单的交互规则,整个种群不存在中心控制,通过个体与个体交互使群体表现出智能的行为特征,就是群智能(Swarm Intelligence,SI)[39]。
粒子群算法(Particle Swarm Optimization,PSO)就是由Kennedy博士和Eberhart博士通过观察鸟类觅食得到启发,提出来的一种新型群智能算法。PSO算法模拟鸟类觅食的过程,将鸟类抽象为粒子,鸟类在觅食过程中某刻的位置,即粒子的位置;鸟类觅食过程中飞行的速度与方向,即粒子的速度矢量;鸟类种群在食物附近飞行觅食的过程,就是粒子种群在搜索空间飞行寻找最优解的过程。通常,在鸟类的飞行过程中,每只鸟都能够记住自己离食物最近的位置,记为个体极值,而整个鸟类群体中离食物最近的那只鸟的位置,记为群体极值。在PSO算法中通过构造适应度函数,可以对每个粒子求其适应度值,得到粒子种群的个体极值与群体极值,在迭代寻优过程中,粒子种群通过追寻个体极值与群体极值来更新种群的速度与位置,最终收敛到最优解的位置。
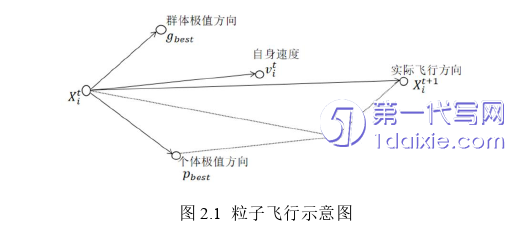
2.2陶瓷配方问题
2.2.1陶瓷配方问题产生背景
陶瓷坯料、釉料是由多种陶瓷原料组成,在过去,由于科学技术发展及生产力限制,人们无法掌握陶瓷坯料、釉料以及陶瓷原料的具体化学组成,在原料获取上,也只能选择当地便于开采获取的陶瓷原料。例如,景德镇因盛产高岭土(又称观音土)、瓷石等陶瓷原料,从而汇聚了大批能工巧匠并建立了景德镇窑,成为了最具有影响力,引领了中国陶瓷业发展的“瓷都”。随着瓷器文化的发展以及古代交通水平的提升,制瓷也不再局限于当地的陶瓷原料,如清代《续文献通考》中提到:“陶土之种类极多,最纯粹者,西人称高岭土。高岭土虽多供输出,用者多来自祁门,祁门南乡龙风壁,西乡伊坑,产量均高,即景德镇所用之上等原料,亦多取于此。”因为祁门瓷土优越的质量性能,大量的运船载着祁门瓷土通过水路由安徽运往江西。不同原产地的陶瓷原料在化学组成上各不相同,在现代化学诞生之前,尽管制瓷工匠们无法理解陶瓷产品的质量性能是由化学组成决定,然而他们可以通过不同原料配比进行一次次烧制实验,通过不断试错及改进,经过大量的生产摸索,总结出包含不同生产原料,烧制工艺的陶瓷配方。
传统的陶瓷配方是由工匠在一次次生产实验中总结出来,其花费的时间长,消耗的成本高,不利于陶瓷产业的规模发展。现代陶瓷应用广泛,包括采矿、航天、医药、精炼、军事、食品和化学工厂、电子行业、工业输电、以及光波导传输等等。例如二氧化锆陶瓷可以用于制造刀具;矾土、碳化硼和碳化硅等陶瓷因为其质量轻,硬度大可以用于防弹背心[50];坦克的复合装甲在中空层填充陶瓷片,利用其硬度大、表面光滑让穿甲弹头发生偏转[51];汽车使用陶瓷刹车片由于其具有良好的热稳定性及机械强度[52];航天飞机、火箭使用陶瓷作为隔热材料[53-54]。陶瓷在现代工业中作为一种优异的功能材料,其用途广泛,这也要求陶瓷制品的生产能够更标准化,规模化,信息化。
第三章 自适应惯性权重及非线性异步学习因子粒子群优化 ............ 13
3.1 引言 .................................. 13
3.2 自适应惯性权重 ................................. 13
3.3 非线性异步变化学习因子 ........................ 13
第四章 APSO算法在陶瓷配方问题上的应用 ......................... 27
4.1 引言 .............................. 27
4.2 陶瓷配方问题模型 .................................. 27
4.3 多目标优化 ....................................... 28
第五章 总结与展望 ................................... 39
5.1 本文总结 ............................... 39
5.2 研究展望 ...................................... 39
第四章APSO算法在陶瓷配方问题上的应用
4.2陶瓷配方问题模型
要运用最优化方法对实际问题求解,需要根据实际问题建立合适的数学模型。为了建立合适的数学模型,通常要经过以下几个步骤:分析确认优化目标(变量),确定约束条件,构造目标函数,选择合适求解方法,计算求解。
(1)确定优化目标
对一般的坯料、釉料进行化学组成分析,可以得到陶瓷坯料、釉料主要由八种氧化物成分组成,包括有SiO2、Al2O3、Fe2O3、MgO、Na2O、CaO、K2O、TiO 2。有些坯料和釉料还含有P2O5等微量元素[63],因为其含量极其稀少且对陶瓷的物理化学性能影响很小,故本文中不再讨论。在实际的陶瓷制品生产中,原料混合成形制成坯体之后,再经过煅烧,其化学组成成分会有所改变,故在对陶瓷配方进行设计时,要对原料进行预处理,求出其减去烧灼量的化学组成质量百分比,下文中给出的目标配方以及原料的化学组成,均已经过预处理,不含灼减量。
多目标优化算法归结起来可以分为两类:传统数学方法及计算智能方法。前者往往将多目标问题转换为单目标问题进行求解。而计算智能方法包括多目标粒子群算法,多目标遗传算法,即是根据问题解空间内可行解的支配与非支配关系,求出Pareto解和Pareto前沿。结合本文4.2节提出的陶瓷配方问题模型,陶瓷配方问题有多个目标函数,如果采用多目标粒子群或多目标遗传算法,会因为其目标函数过多无法判断可行解之间的支配与非支配关系,导致无法求出Pareto最优解。因此本文选取线性加权法将多目标问题转换为单目标问题,再使用APSO算法进行求解。
第五章总结与展望
5.1本文总结
本文主要研究了PSO算法在陶瓷配方问题上的应用求解。首先介绍了粒子群优化算法的基本原理、诞生及发展过程,并详细阐述了粒子群算法中几个重要参数:惯性权重w,学习因子c1,c2在算法寻优中的性能影响。其次,本文在国内外众多学者研究基础上,针对粒子群算法在搜索后期收敛速度慢,易陷入局部极值等缺点,提出了自适应惯性权重及非线性异步学习因子粒子群优化算法(APSO)。该算法通过引入全局极差值,对粒子种群中每个粒子的惯性权重进行自适应变化,当粒子适应度值越接近全局最优值时,可以判断此粒子更需要对其邻近区域进行探索,当粒子适应度值越接近全局极差值时,可以判断此粒子更需要扩大其搜索范围。此外,对于学习因子的改进,标准粒子群优化算法使用的是固定且相等的学习因子c1,c2,考虑到算法前期粒子种群需要更多注重自我认知,算法后期需要更多注重群体认知。在此,本文提出了一种非线性异步变化的学习因子改进策略,c1随着进化过程逐渐变小,c2随着进化过程逐渐变大,从而增强算法前期的全局搜索能力及算法后期的收敛速度。使用标准测试函数对所提出的APSO算法进行测试,测试结果表明APSO算法在寻优精度,收敛速度,稳定性上均有显著的性能提高。
此外,本文将APSO算法应用于陶瓷配方问题求解,详细描述了陶瓷配方问题的基本概念及其数学模型,针对陶瓷配方问题优化中优化目标多,优化难度大等问题,使用线性加权法,并结合Critic法对陶瓷配方中主要化学成分赋权重值,将多目标问题转换为单目标问题,使用APSO算法进行求解。在具体的仿真实例计算中表明,APSO算法相比于其他算法得出的计算配方其主要化学成分的相对误差和更小,其配方精度更高。
参考文献(略)
