本文是一篇计算机论文,本文的研究成果将为量子纠缠态GHZ态提供新的理论支持,促进并深化量子纠缠态的应用,具有重要的理论价值和广泛的应用前景。
第1章 引言
1.1 研究背景及意义
量子纠缠态是重要的物理资源,在量子理论研究中扮演重要角色,可灵活应用于量子通信、量子密码学和量子计算领域。量子纠缠是量子系统的一种非局域关联性质,主要表现为在纠缠体系中对任何一个子系统的测量都会影响其他子系统的状态。
早期对于量子纠缠态的研究大多是停留在哲学层次上的探讨,直至1964年贝尔提出著名的Bell不等式,使得量子纠缠态可通过实验来验证。1969年,Clauser等人得到更易于验证的CHSH型Bell不等式。1982年,Aspect小组利用纠缠光子实验首次验证量子纠缠,也被称为EPR思想实验最为著名的检验。Bell不等式描述两粒子纠缠,不仅仅两个粒子可以处于纠缠态,多个粒子同样可以处于量子纠缠态[1]。1989年,Greenberger,Horne,Zeilinger研究量子纠缠态得到GHZ态。在量子信息论领域中GHZ 态至少包含三个子系统,如三粒子GHZ态,四粒子GHZ态等。2000年,W.Dur等人[2]在研究三粒子系统时发现两种不同类型的纠缠态—GHZ态与W态。
目前,很多研究人员结合量子纠缠态在量子通信领域取得了很多研究成果,例如利用纠缠态设计量子对话(Quantum dialogue,QD)[3-7],实现多方量子密钥协商(Quantum key agreement,QKA)[8-11]以及量子隐形传态(Quantum dialogue,QT)[12-16]等等,但这些成果主要基于量子纠缠态的纠缠性质,缺乏对纠缠态和测量值之间关系的系统分析。为进一步探索量子力学和量子理论国内外学者引入测量来描写纠缠态子系统之间的关系,对量子纠缠态的测量开展了大规模研究,并提出量子纠缠态测量分析。
1.2 主要研究内容
如图1.1所示,论文主体由量子纠缠资源,GHZ态物理理论结合量子同态加密技术和量子密钥协商技术进行研究。此外,GHZ态纠缠资源也可结合量子密钥分发技术与量子密钥回收技术展开应用。主体结构包括第二部分基础理论介绍,第三部分与第四部分GHZ态理论扩展,第五部分与第六部分量子纠缠资源分别与量子全同态加密技术、量子密钥协商技术结合展开应用。
论文的主要研究内容归纳为四个方面:
(1) 研究三粒子GHZ态测量性质扩展
首先研究量子纠缠资源三粒子GHZ态,结合EPR态与单个qubit构造GHZ态,系统地分析八种GHZ态纠缠交换前后状态和测量等性质,提出并计算张量积证明满足纠缠交换的性质。
(2) 研究可扩展的多粒子GHZ
在三粒子GHZ态研究基础上进一步分析四粒子GHZ态的十六种表达式,结合三粒子GHZ态的构造规律构造出四粒子GHZ态,系统地分析四粒子GHZ态初始态和交换后测量所满足的性质,通过计算张量积证明四粒子GHZ态满足的表达式,实现高效量子密钥协商。
(3) 结合量子全同态加密技术实现云中隐私数据计算可用性
当前云计算面临的难题之一是如何在数据计算过程中保证数据私密性的同时又保证数据可用性?本文在量子信息处理的背景下提出了一种量子全同态加密方案,可有效解决云计算所面临的难题。该方案利用GHZ-like纠缠态构造加密密钥,使用量子一次一密实现数据加密,量子逻辑门构造通用量子电路实现任意量子变换,通过执行密钥更新算法得到解密密钥,评估算法独立于加密密钥且加密密钥不同于解密密钥。量子全同态加密技术能够在不解密的情况下对密文数据进行计算,无需破坏敏感源数据并对数据进行处理,实现了云计算领域用户隐私数据计算的可用性。安全性分析和复杂性分析表明该方案适用于隐私数据处理。
第2章 基础理论
2.3基于量子全同态加密的云隐私数据计算基础理论
2.3.1 参与者
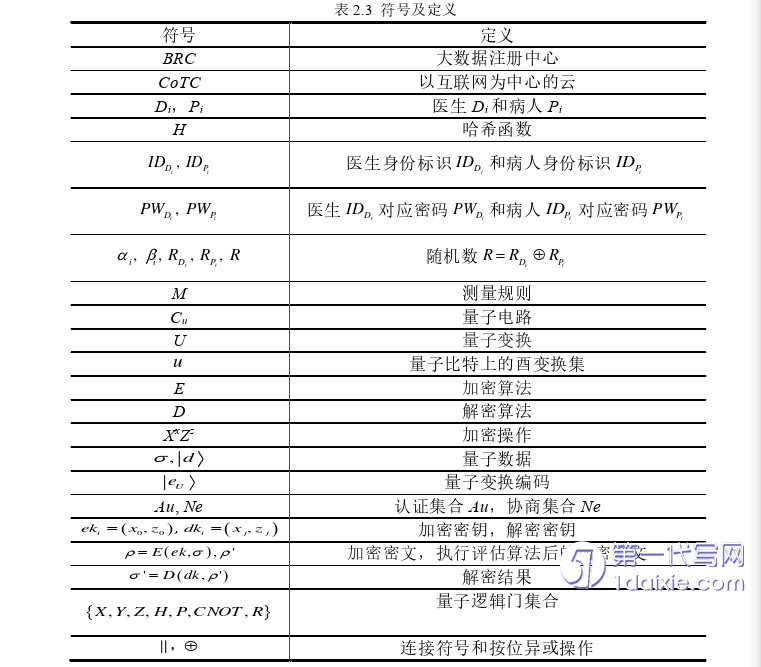
第5章使用的符号及其定义见表2.3,量子全同态加密中包括BRC,iP,iD和CoTC。BRC负责iP和iD注册并为提供iP和iD对应R,将iP和iD的伪身份信息存储于CoTC,iP负责制备三粒子GHZ-like态并发送部分粒子序列给iD,iP和iD根据三粒子GHZ-like态的纠缠性质获取初始加密密钥iek。iP利用iek加密数据发送给CoTC,CoTC结合BRC的伪身份信息验证iP,执行量子全同态加密计算,iP和iD持有iek同步更新,最终iP和iD得到解密密钥idk。
4.9具体应用
4.9.1 两方量子密钥协商
两方量子密钥协商以4.1的公式(4.2)为例,Alice和Bob利用四粒子GHZ态来获取相同会话密钥ABK。Alice和Bob事先已面对面安全共享初始密钥IK,IK是一串长为N的二进制数决定测量基底,具体测量规则见表4.1,其中IKi=0表示第i位使用X-basis测量,IKi=1表示第i位使用Z-basis测量(i=1,2,3,...,N)。具体包括StepA,StepB,StepC三个步骤。
Alice和Bob测量单光子态D执行安全检查。Alice根据Bob提供的4bS序列中单光子态信息随机选择一些单光子态D进行测量,同理Bob根据Alice提供的4aS序列中单光子态信息随机选择一些单光子D进行测量。随后,Alice和Bob通过传统信道告知对方单光子的测量结果,双方根据对方的测量结果计算错误率,如果错误率高于某个阈值则表明存在窃听者,此时应重新执行StepA,重新制备GHZ态,反之则进行下一步。
第3章 三粒子GHZ态性质扩展及证明 ................................ 14
3.1 两组GHZ态交换一个粒子 ................................ 14
3.2 两组GHZ态交换两个粒子 ........................................ 15
3.3 三组GHZ态交换一个粒子 ................................ 15
第4章 可扩展多粒子GHZ态方程与高效量子密钥协商 .................. 22
4.1 两组GHZ态交换一个粒子 ........................ 22
4.2 两组GHZ态交换两个粒子 .................................. 23
4.3 三组GHZ态交换一个粒子 ................................. 24
第5章 基于量子全同态加密的云隐私数据计算 ......................... 34
5.1 注册阶段 ................................. 34
5.1.1 医生注册 ............................................... 34
5.1.2 病人注册 .............................................. 34
第5章 基于量子全同态加密的云隐私数据计算
5.1 注册阶段
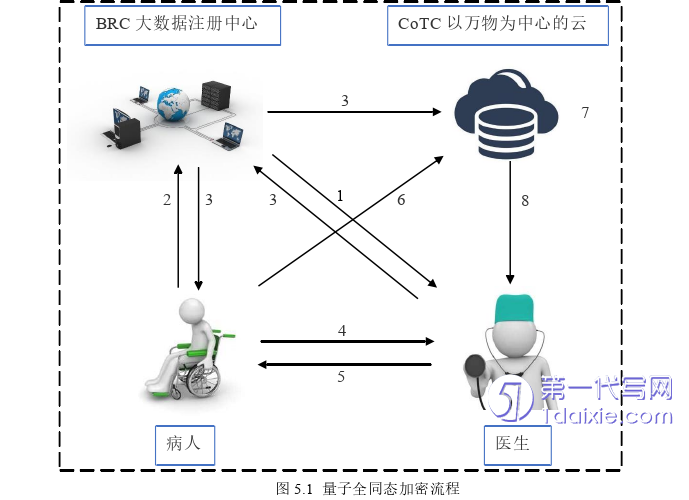
基于量子电路uC构建了一个量子全同态加密规则,具体包括五个阶段:注册阶段,密钥生成阶段,加密阶段,评估阶段,解密阶段。图5.1展示了量子全同态加密规则整体流程,不同阶段对应不同的数字,注册阶段对应数字1,2,3,密钥生成阶段对应数字4和5,加密阶段对应数字6,评估阶段对应数字7,解密阶段对应数字8。
第7章 总结与展望
GHZ纠缠态是量子安全通信中不可或缺的重要资源,利用GHZ态可实现量子密钥共享[76]、量子密钥分发[79]、量子秘密共享[80]等。本文主要分析三粒子GHZ态与多粒子GHZ态交换测量性质,结合GHZ态和量子全同态加密技术实现云隐私数据计算以及量子密钥协商。
在第3章和第4章GHZ态性质扩展及证明部分,先分析两组GHZ态、三组GHZ态、四组GHZ态交换一组粒子和两组粒子,证明交换后测量的粒子满足部分公式,通过归纳得到多组GHZ态交换一组粒子和两组粒子所满足的公式。在第5章云隐私数据计算中,在量子信息处理的背景下利用GHZ-like态构造加密密钥,进一步结合量子全同态加密技术实现云环境中用户隐私数据计算的可用性与数据私密性。在第6章量子密钥协商中,利用GHZ态实现三方交互认证,结合泡利操作实现三方密钥共享,最后安全性分析和效率分析表明该协议能够有效抵抗常见攻击,具有可行的效率。
本文虽然只着重分析GHZ纠缠态交换测量后满足的关系,但是量子纠缠资源的研究课题相当广泛,还有很多相关理论与现实应用值得进一步研究。2019年,石润华研究了Bell态纠缠交换,并进一步证明Bell态所满足的公式;在此基础上本文研究了GHZ态纠缠交换,并进一步证明GHZ态所满足的公式;除了Bell态和GHZ态,W态和Cluster态也是重要量子纠缠资源,那么会很自然的联想到W态和Cluster态是否也像Bell态和GHZ态一样满足纠缠交换测量公式?如何根据纠缠资源的测量特性推出满足纠缠交换的公式是一个重要的研究方向,倘若W态和Cluster态等纠缠资源满足相关公式,能否借助纠缠态的测量推出新的理论并将其运用于特定领域?
参考文献(略)
