本文是一篇计算机论文,本文研究并设计了三种秘密共享方案:重构结果可验证的(t,t)门限秘密共享方案,门限可变的(i,Mi,t)多层次秘密共享方案,(i,j,Mj,tj)多层次多秘密共享方案;分析了这三种方案的实际性能,包括准确性、安全性、存取结构、公开值数量等,说明本文所设计的方案在构造方法、通信效率等方面有所改进。
第1章绪论
1.1研究背景及意义
应用密码学技术的过程,就是隐藏信息的过程。由于密码学过于特殊,在不同时期,人们都热忱于研究密码学技术[1,2]是如何使用的。以发展方向为依据,密码学大致可以分为两种:其一为古典密码学,另外一种为现代密码学;以研究内容为依据,其可分为两个流派[3]:其一为编码学,另外一种为破译学。在目前的密码学研究中,通常以数学手段研究信息是如何传输的。研究内容发展的同时,密码分析学也获得了一定程度的发展,现在的研究目的不再仅限于加密信息,还要实现一些实际需求,如控制访问者权限、识别参与者身份、抵御内外部攻击等。特别地,在保障信息安全方面,密码学做出了巨大贡献。这也要求密码学技术不断更新,保证信息安全性、完整性的同时,还能鉴定参与者身份,只有具备了这些基本功能,该密码技术才能称为安全技术。
随着信息技术的发展,利用互联网交换信息的行动越发频繁,数据信息这一资源的社会地位越来越高。5G时代的到来,也带来了信息爆炸,信息价值越发瞩目。同时互联网技术的普及,进一步推动信息交互特点的形成,如互联性、开放性。在这一情况下,个人、企业甚至国家信息泄露事件频发,且造成的损失巨大,如何保障信息安全已成为难题。分析现阶段出现的信息安全事件,现代密码学提出了一系列技术尝试解决问题,如身份认证、信息加密、数字签名等。这些加密技术的实现,关键是可以很安全的保存密钥,一旦某一技术无法保障密钥安全性,其也就失去了竞争价值。在众多加密技术中,秘密共享技术占据了重要位置,该技术主要解决密钥泄露事件。
1.2研究现状
1.2.1秘密共享方案研究现状
秘密共享方案也被称为秘密共享安全协议,其成立的基础是分发与重构算法,也就是方案要成立在“秘密共享体制”上。关于“秘密共享体制”,其最早出现在1979年,由Shamir[1]和Blakley[2]两人提出,学者们以这一体制为基准进行了更深入的研究,或在原有方案上改进,或提出利用新思路实现秘密共享的方案。1983年,基于中国剩余定理Asmuth[4]等人提出了一种新的门限方案,该方案的成立利用了同余类思想,可以在线性时间内实现秘密重构这一功能,比Shamir[1]方案更高效。1989年,Brickell[5]利用向量空间这一数学知识,构造了此种类型的访问结构秘密共享方案,该方案是Shamir[1]方案的更一般形式。基于这一思想,Padro[6]等人于1999年提出秘密共享方案,在该方案中,参与者份额由向量构成,因此在重构阶段可检测到是否存在不诚实成员。但该方案成立要具备一个前提,即秘密分发者是可信的,且重构构成安全无攻击。1983年,Karnin[7]等人利用矩阵运算规律,提出一种门限方案。该方案成立在克拉默法则上,即在对由一个矩阵构成的线性方程组求解时,只有该矩阵是满秩的才能求出唯一解,这也是重构的秘密唯一性的前提保证。在1985年密码学年会上,Wolfram提出了一种新的秘密共享方案设计思路,即在方案中引入细胞自动机:一种随机数发生器设计方法,该方法还可用于设计流密码,这一想法引发了学者们对于该方法应用到秘密共享方案创建中的尝试。此后,庞辽军[8]等人基于Wolfram的秘密共享方案设计思想,设计了一种基于一维细胞自动机的方案。
1989年,Ito[9]等人突破了特殊门限的限制,设计一种访问结构更一般的秘密共享方案。在该秘密共享方案中,参与者权限不再是理想的、平等的,而是结合现实社会,为参与者权限赋予了个性,更适合应用于实际使用中。2016年,顾为玉[10]等人提出了一种可验证的秘密共享方案,该类方案建立在二元对称多项式数学基础上。在重构秘密时,利用离散对数困难问题可验证份额,并可异步环境下实现秘密恢复,但是该方案并没有给出详细的加密步骤。2017年,Harn[11]等人基于二元多项式,提出一种多秘密共享方案,该方案主张多秘密异步重建思想,在恢复秘密时不泄露已恢复秘密的任何信息。对此,2018年Zhang[12]针对Harn[11]多秘密共享方案提出改进意见,并给出解决措施。同年,郝星然[13]等人也利用二元多项式,提出了一种可异步恢复的秘密共享方案,同时该方案还可以抵抗内部攻击,保证了前期重构秘密的安全性。
第2章预备知识
2.1数学基础知识
本节主要介绍一些数学知识,包括拉格朗日插值法、克莱姆法则、中国剩余定理等三方面。
2.1.1拉格朗日插值法
拉格朗日插值法(Lagrange Interpolation Polynomial)简记为LIP,1795年正式出现在约瑟夫·路易斯·拉格朗日的著作中,是一种用来分析数值的多项式插值法。利用该方法构造的拉格朗日多项式,可呈现数据间内在的联系或规律,具体表示如下。
定义2.1.拉格朗日插值多项式:已知某多项式的若干个点,利用拉格朗日插值法可得到一个插值多项式,该多项式称为拉格朗日插值多项式。在二维平面任取一个t−1次多项式,由其上t个不同的数据对{(x1,y1),···,(xt,yt)},可获得唯一的t−1次多项式f(xi),且f(xi)=yi,其中1≤i≤t;若t−1次多项式上任意n个不同的数据对{(x1,y1),···,(xn,yn)}构成集合P={(x1,y1),···,(xn,yn)},在集合P中随机取t个子集合(xi,yi),其中1≤i≤n,利用公式2.1可获得唯一的t−1次多项式
2.3秘密共享简介
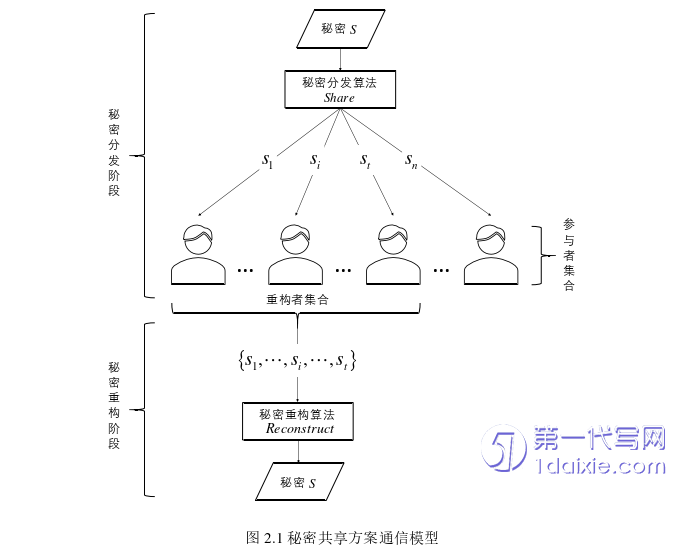
2.3.5秘密共享模型
在(t,n)秘密共享方案中,通常会出现三类成员:
(1)秘密管理者(Dealer):又称为秘密分发者,负责构建秘密共享方案,涉及选择秘密值、确定参数、生成并分发秘密份额等工作;
(2)秘密参与者(Participant):又称为份额持有者(Shareholder),会收到管理者分发的秘密份额,并秘密持有该秘密份额。当需要参与秘密重构时,将所持份额发送给重构者;
(3)秘密重构者(Reconstructor):在秘密重构阶段,秘密重构者收到参与者发送的秘密份额,并利用秘密份额重构秘密。一般来讲,秘密共享方案不需要构建单独的秘密重构者,每个参与者都可以承担秘密重构工作,通过共享秘密份额的方式获得秘密重构所需信息。
第3章可验证的秘密共享方案...................25
3.1形式化定义..........................................25
3.1.1可验证秘密共享模型.........................25
3.1.2设计目标..................................26
第4章门限可变的多层次秘密共享方案......................34
4.1形式化定义................................34
4.1.1分层秘密共享模型..............................34
4.1.2设计目标....................................36
第5章多层次多秘密共享方案及其应用.........................48
5.1形式化定义.............................48
5.1.1多秘密共享模型...........................48
5.1.2设计目标.....................................49
第5章多层次多秘密共享方案及其应用
5.1形式化定义
5.1.1多秘密共享模型

秘密共享方案由初始化、秘密分发、秘密重构三部分构成,并由分发者、参与者两类实体协同完成,其中分发者为可信实体、参与者承担重构秘密的责任。
5.1.1.1初始化
分发者选择要分享的秘密;选择构造多项式的参数,并对求该多项式的i次微分公式;随机生成一个安全可碰撞哈希函数;选择tj个整数m1,···,mtj。
5.1.1.2秘密分发阶段
(1)身份标识生成:参与者生成身份标识并公开,不同参与者身份标识不同。(2)公开值生成:分发者根据参与者身份标识计算对应多项式,一部分秘密发送参与者作为用户秘密值,另一部分利用中国剩余定理聚合部分数值形成公开值;用哈希函数为秘密生成散列值,利用随机值与异或算法生成秘密转换值,并公开信息。(3)子份额分发:分发者通过安全信道传递秘密份额。
5.1.1.3秘密重构阶段
(1)足够数量的子参与者参与信息共享,以保证子份额数量满足阈值,利用中国剩余定理从公开值中获得信息,从而获得部分秘密份额,然后利用这些已知信息与微积分算法获得剩余的秘密份额。(2)根据公开转换值与秘密份额异或计算,从而获得秘密。(3)结果验证阶段:参与者获得秘密后,可与公开的秘密哈希值比较验证。
第6章总结与展望
6.1总结
本文研究并设计了三种秘密共享方案:重构结果可验证的(t,t)门限秘密共享方案,门限可变的(i,Mi,t)多层次秘密共享方案,(i,j,Mj,tj)多层次多秘密共享方案;分析了这三种方案的实际性能,包括准确性、安全性、存取结构、公开值数量等,说明本文所设计的方案在构造方法、通信效率等方面有所改进。本文完成的工作如下:
(1)分析研究现有的秘密共享方案,特别是经典的(t,n)秘密共享模型,了解该类方案的创建思想后,提出了一种建立在微积分算法上的(t,t)可验证秘密共享方案。正确性、安全性分析表明该方案是一个完善的秘密共享方案,秘密份额数量达到门限值能正确恢复秘密,若秘密份额数量不满足门限值,则无法重构秘密,同时在秘密份额传输时应用RSA算法加密,可有效抵抗外部攻击;验证性分析表明利用单向哈希函数计算秘密产生散列值,用于验证重构结果正确是可行且有效的;性能分析表明该方案可在多项式时间内执行完毕,通信成本可控。
(2)分析研究现有的多层次秘密共享方案,认识到要想实现参与者多级别共享秘密,可根据参与者重要性差异,为其赋予特定的权限,提供对应的秘密共享门限值,对此本文提出了一种门限可变的(i,Mi,t)多层次秘密共享方案。在该方案中,只要参与者秘密份额满足门限要求,就可以根据自身对应的公开信息恢复秘密,经正确性分析发现这一访问结构是成立的,安全性分析表明若秘密份额不满足门限值是无法重构秘密的。验证性分析表明利用单向哈希函数计算秘密产生散列值,用于验证重构结果正确是可行且有效的;性能分析表明该方案可实现门限可变功能,可根据参与者层次调整门限值,比门限固定的方案计算量更小,成功体现了不同层次参与者的优先级差异性,而且公开信息的生成,可减少需加密传递的信息量,通信效率更高。
参考文献(略)
