本文是一篇计算机论文,本文基于PCNN模型对电梯内电瓶车进行识别,通过对PCNN的参数寻优,以此来平衡识别算法的性能和精准度。
第一章 绪论
1.1 研究背景及意义
近年来,我国生产总值持续增长,城镇化发展迅速,为充分发挥国土土地单位面积利用率,高层民用建筑成为城市建造中的主流。随之而来的是,部分居民将电瓶车违规带入高层民用建筑,使用老化电线、劣质充电器或者私接电线给电瓶车充电。在高层建筑中,这种行为是引发火灾的主要原因之一。为了有效避免电瓶车违规进入高层民用建筑,保障居民的生命财产安全,应用人工神经网络对电梯内的电瓶车识别是一种较为可行的方法。
人工神经网络发展至今,具有相当成熟的理论基础,并且作为融合生物信息学、计算机科学、数学和电子学等多方面的综合学科,在模式识别、机器学习、预测估计和图像处理等领域应用广泛。自最初的MP模型[1]( McCulloch-Pitts model, MP)建立以来,人工神经网络经历了七十多年的演变,产生出许多数学模型,如多层感知机[2]、Hopfiled网络[3]等。当前,人工神经网络的模型更加趋于模拟哺乳动物神经网络来建立。
脉冲耦合神经网络(Pulse Coupled Neural Network,PCNN)[4-5]于20世纪90年代初期诞生,是一种模拟哺乳动物的视觉皮层功能建立起来的第三代神经网络模型,该网络自身具有提取图像基本组成成分的能力,且输出的图像对平移、旋转和尺度收缩、扭曲具有强鲁棒性。PCNN属于单层神经网络,外部激励相似的神经元会同步受到激发,省去了训练调整的步骤,提高了图像分割和边缘特征提取的运行效率。当神经元被激发释放脉冲时,PCNN会将图像这种二维空间向量转换为一维时间脉冲,这种行为与生物体中神经元释放信号十分相似,这也使PCNN比传统的人工神经元更接近实际神经网络。不仅为当前人工智能模型的优化开辟了另一条通道,而且促进了生命科学中生物神经网络的研究。脉冲耦合神经网络的高效性、强适应性和良好的可解释性,使其将成为未来人工神经网络发展的方向。
1.2 国内外研究现状
1.2.1 PCNN研究现状
自1996年以来,一系列简化的PCNN被相继提出,比如Kinser[12]提出了一种与PCNN在图像处理方面效果极为相近的简化模型,交叉皮层模型(Intersecting Cortical Model, ICM)[13]。Zhan等[14]于2009年提出了一种发放皮层模型(Spiking Cortical Model, SCM),该模型在保留PCNN模型生物学的基础上,对其数学公式做了极大简化。2011年,Chen等[15]人提出了一种基于参数自动设置的简化PCNN模型的图像分割及其在目标识别上的应用,简化了原有的大量参数,但是对边缘特征提取的效果不理想。Yang等[16]提出了一种基于PCNN的非整数步长指数模型,当该模型在处理极高离散问题时,可得到高精度解。因而,该模型成功地应用在处理乳腺钼靶X图像钙化点方面。Lian等[17]为了克服PCNN模型参数繁多的弱点,在一种基于简化脉冲耦合神经网络(Simplified Pulse Coupled Neural Networks, SPCNN)的基础上提出了一种修正的简化脉冲耦合神经网络模型(Modify Simplified Pulse Coupled Neural Networks, MSPCNN)。文献[18]由于PCNN时间信号不受图像平移、缩放、旋转和光照变化等的影响,提出了基于PCNN的时间信号特征。文献[19]提出了一种新型双输出脉冲耦合神经网络模型,验证了该模型在几何变量纹理检索方面优于现有模型。文献[20]利用阈值分割得到一系列二值图像,提取二值图像的分形维数特征对医学图像进行分类。此外,他还提出了双门分割[21],这在医学图像、遥感图像和纹理图像的分类方法中是有效的。
第二章 PCNN模型发展历程
2.1 同构模型
同构模型是在原始PCNN的基础上,使用的参数和结构不发生改变,发生改变的只是原始神经元内部的连接方式。本章将介绍两种常见的PCNN同构模型,一种是全连接PCNN,另一种为ICM。
2.1.1 全连接PCNN
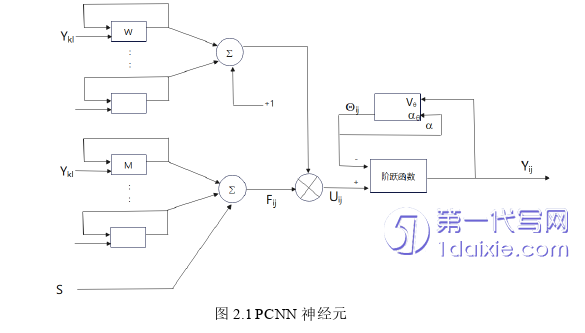
由生物学研究可知,神经元细胞由细胞体和突起构成,突起由树突和轴突两部分构成,神经元的突起是接收上一神经元释放的信号,接收到的信号在神经元内部处理过后,又将信号由突触释放给周围有多个其他神经元的突起。神经元细胞作用就是接收刺激、产生兴奋并传导兴奋。一个PCNN结构就是依据单个的生物体神经元建立而来。PCNN神经元带有突触权值的馈入输入和连接输入,经过内部的动态阈值发出点火信号,触发到周围神经元和自身并输出脉冲信号。因此,全连接PCNN中参数不像多层神经网络,需要通过消耗庞大的计算量去训练参数,根据实际情况设定参数即可达到良好的处理效果。
2.2 异构模型
异构PCNN模型由于是在原始PCNN上改变初始参数的值,所以与同构模型相比更加真实地模拟生物神经元的运作和连接方式。本章概述了三种常见的关于PCNN的异构模型。
MSPCNN模型[40]如图2.5所示,MSPCNN模型在减少原始PCNN模型参数的同时优化了其中的参数,MSPCNN的反馈单元中的设置于SPCNN相同,只有一个外部激励,但是不同之处在于阶跃函数Xij的设置有所不同。MSPCNN不仅确定了最优迭代步数,而且解决了最优特征的值等于1的这一问题。
构建基于PCNN的电梯内电瓶车识别模型的主要步骤分为图像分割、特征提取和分类识别,整体研究框架如图3.1。其中,模型中图像分割算法是根据PCNN神经元同步激发的性质,产生基于输入图像的整块状的分割区域,在此基础上设定触发机制和分割后的迭代终止条件。模型中特征提取算法是将分割后的图像灰度值与仿射不变矩结合,使在电梯背景下的电瓶车,不再受到成像时因丢失一维信息发生的畸形变化,可提取相对完全的电瓶车特征。最后,模型的分类识别是结合粗糙集和支持向量机建立分类器,在电梯场景下实现对电瓶车的识别。
第三章 基于PCNN的电梯内电瓶车识别 ............................ 15
3.1 基于PCNN的电梯内电瓶车图像分割 ...................................... 15
3.1.1 基于均方差的PCNN外部激励 ................................. 15
3.1.2 基于最大模糊散度的PCNN迭代条件 ........................... 16
第四章 基于SOAEV-PCNN的电梯内电瓶车识别 ........................... 37
4.1 标准的海鸥优化算法 ............................ 37
4.1.1 迁移算子 ................................... 38
4.1.2 捕食算子 ................................ 38
第五章 基于CRSOAEV-PCNN的电梯内电瓶车识别 ...................................... 47
5.1 融合Cubic混沌和折射反向学习的海鸥优化算法 ............................. 47
5.1.1 基于Cubic映射的种群初始化 ................................. 47
5.1.2 参数A的改进 ....................................... 48
第五章 基于CRSOAEV-PCNN的电梯内电瓶车识别
5.1 融合Cubic混沌和折射反向学习的海鸥优化算法
5.1.1 基于Cubic映射的种群初始化
为丰富种群多样性,避免个体陷入局部最优解,有效地提高寻求最优解的概率,利用混沌映射进行种群初始化。
Cubic混沌[74]映射作为常见的混沌映射方法之一,具有较好的混沌遍历性
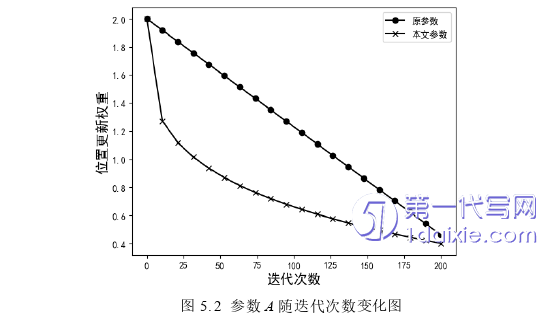
改进的参数A为非线性递减函数,迭代初期参数值变化速度较快且数值较大,有利于提高算法的收敛速度。算法迭代后期,参数A在较长时间内保持较小的数值且变化速度逐渐减缓,加强局部搜索中勘探新解的能力,提升算子的解精度。引入的beta可使粒子发生局部扰动,增加种群多样性。原参数A与改进后的参数对比如图5.2所示。
第六章 总结与展望
6.1 总结
电瓶车进入高层民用建筑引发的火灾,严重危害到居民的人身财产安全。检测电梯内电瓶车的需求已经引起了我国相关部门的高度重视。基于图像的识别技术是城镇防火的重要研究方向,当前图像识别技术多采用神经网络中卷积神经网络、U-Net网络、BP神经网络和LVQ神经网络等,但这些方法前期需要进行大量的训练,且有可能降低识别算法的寻优能力。为此本文基于PCNN模型对电梯内电瓶车进行识别,通过对PCNN的参数寻优,以此来平衡识别算法的性能和精准度。具体工作总结如下:
(1)对电梯内电瓶车识别的研究背景及意义进行了说明,对目前神经网络、PCNN模型及基于PCNN模型的应用研究现状进行了总结。介绍了PCNN模型的一些相关概念,分别介绍了基于PCNN的同构模型和异构模型。
(2)构建基于PCNN的电梯内电瓶车识别模型(EV-PCNN)。在原始PCNN中引入均方差作为外部激励,原始图像的像素值在均方差的平衡下,避免点火时由于像素值相差过大,出现误分割现象。将最大模糊散度作为终止迭代条件,计算目标图像与背景图像的隶属度,从而将目标图像准确、快速的从原始图像分割出来。与AMI结合提取不同类型且不同尺度变换的电瓶车特征。将粗糙集理论引入SVM,提高识别效率。经过实验证明,该识别模型满足电梯背景下电瓶车监测的实时性强、准确率高等要求。
(3)针对EV-PCNN模型出现的参数多、难以设置及对结果影响较大的问题,提出了一种基于海鸥优化算法对PCNN的参数进行优化。该算法分为两个阶段以线性搜索为主的迁移阶段和螺旋式的捕食阶段,用于优化EV-PCNN中PCNN的初始权值。经测试函数验证,SOA在解决较高维问题时存在求解精度低、收敛速度慢等缺陷,但SOAEV-PCNN模型识别电梯内电瓶车的准确率和效率比EV-PCNN优秀。
参考文献(略)
