本文是一篇计算机论文,本文构造的方案都仅限于选择性安全模型,如何设计出更强的适应性安全方案是今后亟待解决的问题。且基于LWE问题的方案存在侧信道内存攻击问题,如何设计出抗泄露的格上多策略属性基全同态加密方案也是今后需要进一步研究的问题。
第一章 绪论
1.1研究背景与意义
随着信息技术的不断发展,现代社会的数据呈爆炸式增长,越来越多的企业和用户将数据存储到云服务器上,云服务器具有强大的功能,不仅能够存储数据,还能够处理数据。云计算作为一种远程服务模式,已成为企业中一种具有成本效益的业务数据解决方案。为了方便企业在第三方数据中心存储和处理数据,云计算提供了多种服务模式,例如,基础设施作为一种服务、平台作为一种服务和软件作为一种服务。虽然云计算提供了众多的商业竞争优势,但是它引起了严重的数据机密性问题。由于企业委托他们的数据访问给第三方云服务提供商 (Cloud Service Provider,CSP),其可滥用访问权限来推测或篡改有价值的信息,从而造成用户隐私泄露等一系列安全问题。为了保护这些外包数据免受未经授权用户的访问,最有效的方法是使用传统的安全机制。例如,在不受信任的第三方上安装防篡改硬件,或者数据在上传到CSP 之前可先进行加密。但是,往往需要对这些加密数据进行一些计算(例如预测分析,回归分析等),而传统密码系统显然不能支持这种计算。全同态加密(Fully Homomorphic Encryption,FHE),不仅满足传统加密的功能,并在无需解密的情况下可对密文进行任意计算,计算的结果解密后,与对明文做相同计算的结果相同。这种性质使得FHE能够在云计算环境下对云端存放的密文进行安全处理,解决了云计算中数据共享安全和计算安全的问题[1]。因此,为了保证共享数据的隐秘性和可计算性,将数据上传CSP之前,企业可使用同态加密方案对数据进行加密。此时,CSP 在无需对加密数据解密的情况下就可对这些加密数据进行计算。
1978年,Rivest[2]等人指出RSA公钥加密方案具有乘法同态性,即在无需解密的情况下可对密文进行乘法操作,操作的结果解密后与对明文做同样的乘法操作相同,但是方案不具有加法同态性。随后,Rivest等人首次提出了全同态加密的概念,即一个可实现任意多项式的加法和乘法计算的技术。然而,实现全同态加密须过五关斩六将,因困难程度较大,被誉为密码学界的“圣杯”[3]。在实现全同态之前,出现了很多部分同态加密方案(Partly Homomorphic Encryption,PHE)[4-14]和近似同态加密方案(Somewhat Homomorphic Encryption,SWHE)[15-19],其中PHE只支持一种同态计算,要么实现加法同态计算,要么实现乘法同态计算,例如著名的ElGamal[6]乘法同态方案和Paillier[7]加法同态方案。
1.2研究现状
1.2.1 格上全同态加密
2009年,Gentry[20]解决了密码学中的核心问题,基于理想格提出了第一个全同态加密方案,在不知道解密密钥的情况下,可计算加密数据的任意多项式函数。首先方案采用电路计算模型来构造了一个SWHE方案,可支持有限次数的同态计算。然后基于稀疏子集和问题“压缩”解密电路,同时通过自举(bootstraping)电路更新密文,使得密文具有更小的噪声,以进一步执行解密函数进行同态解密来实现任意多项式的同态计算,最后在循环安全假设下证明了方案的选择明文攻击(Chosen Plaintext Attack,CPA)安全性。然而由于方案需要自举程序实现,使得私钥生成和加密开销较大,同态解密的效率较低,故方案效率比较低。随后,为了提高全同态加密方案的效率,在Gentry方案的基础上,出现了许多优化FHE方案。Smart[28]等人提出了具有更小密文和私钥的FHE方案。Gentry[29]等人提出了更优的自举程序,为了减小私钥尺寸,方案使用主理想格的代数结构代替原本抽象的理想格结构,进一步提高了FHE的效率。Stehlé[30]等人利用“可忽略概率解密错误”这一弱化条件改善了Gentry提出的方案,提出了较快的FHE方案。
2011年,Brakerski [31]等人打破了Gentry构建的FHE方案的框架,提出了基于Ring-LWE(Ring-Learning With Error)问题的FHE方案,首先构造了一个SWHE方案,然后结合Gentry的压缩解密电路和自举技术将SWHE变为FHE方案。同年,Brakerski[32]等人提出了基于标准LWE问题的FHE方案,方案在Regev[33]方案的基础上,利用重线性化技术将其修改为SWHE方案,然后利用维数-模数约减技术代替压缩解密电路技术,无需再依赖稀疏子集和假设,从而缩减了密文尺寸以及降低了解密电路的复杂度。然而,该方案仍需要自举程序才能实现真正的FHE方案,效率有待提高。2012年,Brakerski[21]等人提出了基于LWE问题和Ring-LWE问题的无需自举程序的层级FHE方案BGV12,方案使用了复杂的密钥交换和模交换技术代替自举程序提升了方案的性能,然而这俩种技术只能在一定程度上控制噪声的增长。同年,Brakerski[34]等人对此进行了改进,利用张量积技术代替复杂的模交换技术来减少噪声的增长,无需通过压缩电路技术来执行同态解密函数进行同态解密。
第二章 支持多跳的格上多策略属性基全同态加密方案
3.1方案的性能分析与实验仿真
3.1.1性能分析
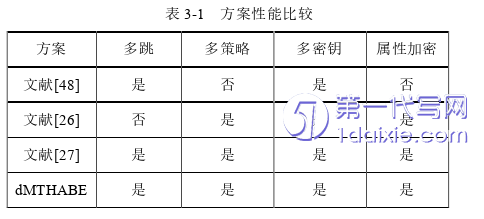
本节首先将本章dMTHABE方案与文献[26]、 [27]、 [48]中的多密钥方案进行性能比较,从多跳、多策略、多属性以及属性加密四个方面来评估,结果如表3-1所示。2016年,Peikert等在文献[48]中提出了两种动态多跳的MKFHE 方案,任何用户都可以动态地加入到密文计算的过程中。其中方案一的特点为密文尺寸较大,而方案二密文相对较短,密文扩展实现较为方便。但该方案是基于公钥,不是属性基加密。Brakerski等人在文献[26]中分别提出了单策略和多策略T-HABE方案, 其中多策略方案可对满足不同策略的密文进行同态运算,但该方案是单跳的,不具备多跳性质,即同态计算过的密文不能再次与新密文进行同态计算。2017年,Hiromasa在文献[27]的多跳 MKFHE 方案一的基础上,提出了具有动态同态计算的多策略ABFHE方案,但该方案和文献[47]的方案一具有相同的密文尺寸较大,密文计算效率不高的特点。而本章是在文献[48]的方案二基础上,提出的具有动态同态计算的多策略ABFHE方案,具有密文短,密文扩展方便以及同态计算效率高的优点。
3.2方案的性能分析与实验仿真
3.2.1方案的性能分析
表4.1对文献[26]、[54]、[57]、[59]、[61]、[64]中的方案、本文第三章提出的支持多跳的多策略属性基全同态加密方案dMTHABE和本章提出的支持多比特的单策略属性基全同态加密方案STMHABE以及支持多比特的多策略属性基全同态加密方案MTMHABE的性能进行了分析。主要从多策略、多密钥、多跳、多比特、属性加密、一次性解密和灵活解密这几个方面进行了比较。
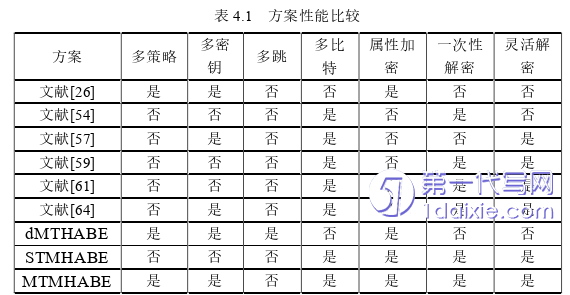
比较结果如表4.1所示,文献[26]方案属于多策略(多密钥)属性基同态加密,但是只能加密单比特消息,同态计算效率低下,且不支持多跳。文献[54]方案属于多比特同态加密,支持一次性解密整个消息,但是不支持灵活解密特定比特位消息,且不支持属性加密。文献[57]方案属于多密钥的多比特同态加密,但是仅支持灵活解密,不能一次解密整个消息,具有较低的实用性,且不支持多跳。文献[59]方案属于多比特同态加密,可一次性解密整个消息,也可灵活解密特定比特位消息。文献[61]方案属于多比特同态加密,支持一次性解密整个消息和灵活解密特定比特位消息。文献[64]方案属于多密钥的多比特同态加密,可一次性解密整个消息,也可灵活解密特定比特位消息,但不支持多跳。本文提出的dMTHABE方案属于多密钥的属性基全同态加密,具有多跳性质,同态计算过的密文可与新密文再次进行计算,但是只支持单比特加密。本文提出的STMHABE、MTMHABE方案是第一个支持多比特的属性基全同态加密方案,其中STMHABE方案能对满足某个单一策略的属性集密文进行同态计算,可一次性解密整个消息,也可灵活解密特定比特位消息。而MTMHABE方案是将STMHABE方案与多密钥同态加密技术结合,可对满足不同策略的密文进行同态运算,但是不具有多跳性质。
第三章 支持多跳的格上多策略属性基全同态加密方案 ....................... 20
3.1方案系统模型 ...................................... 20
3.2方案的形式化定义和安全模型 ........................ 21
第四章 支持多比特的格上多策略属性基全同态加密方案 .............................. 36
4.1方案系统模型 ......................................... 36
4.2支持多比特的格上单策略属性基全同态加密方案 ................... 38
第五章 总结与展望 .......................... 65
5.1总结 ..................................... 65
5.2展望 ................................ 66
第四章 支持多比特的格上多策略属性基全同态加密方案
4.1方案系统模型
支持多比特的格上单策略目标属性基全同态加密方案STMHABE只可以对属性满足某个单一策略的密文进行同态计算,而在支持多比特的格上多策略目标属性基全同态加密方案MTMHABE 中,一组策略与同态计算相关,可以在属性满足策略集合中某个策略的密文之间进行处理。因此STMHABE和MTMHABE方案的系统模型基本一致,区别在于STMHABE中的能够解密的用户的访问策略单一,即能够解密的用户拥有相同的私钥,解密不需要联合所有用户私钥。
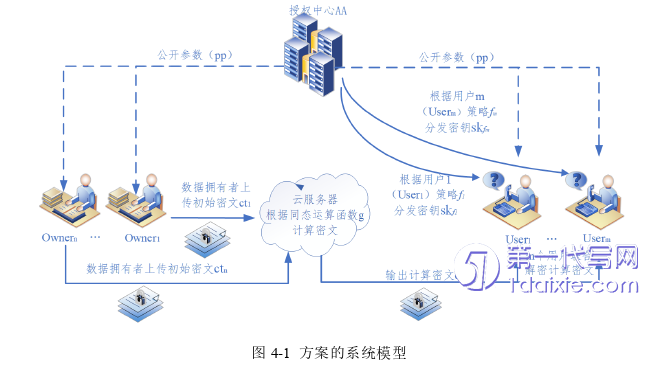
方案的系统模型如图4-1所示,由属性授权中心(AA)、数据提供者(Owner)、数据访问者(User)、云服务提供商(Server)四个实体构成。它们各自的职责如下:
(1)AA:授权中心是一个完全可信的实体,负责管理系统中的属性,拥有整个系统的公共参数和主密钥,根据每个User的访问策略来为其分配密钥。
(2)Owner:数据提供者拥有属性集,根据属性集加密共享数据,生成共享数据密文,并将其上传到Server上。
(3)User:数据访问者拥有访问策略,从AA得到与策略相关的密钥。从Server接收到处理密文,如果密文的属性集满足User的访问策略时,则可以解密该密文。
(4)Server:云服务提供商是一个诚实但好奇的半可信实体,Server会好奇存储在云上的数据,但是绝对忠诚,会严格履行特定的服务,不会恶意删除数据或者拒绝响应User的请求。在本系统中Server主要负责将Owner上传的数据进行同态计算,得到同态计算密文。
第五章 总结与展望
5.1总结
随着信息技术的不断发展,现代社会的数据呈爆炸式增长,越来越多的企业和用户将数据存储到云服务器上,云服务器具有强大的功能,不仅能够存储数据,还能够处理数据。云计算作为一种远程服务模式,已成为企业中一种具有成本效益的业务数据解决方案。为了保证用户隐私,防止数据的泄露,数据通常被加密后存放在云端。FHE技术既可满足传统加密的功能,又可在不知道密钥的情况下,对密文进行任意计算。但是只能对相同公钥(用户)下的密文进行计算以及不能实现对共享数据的细粒度访问控制。ABFHE技术可在实现对加密数据细粒度访问控制的的同时,又可对同属性集密文进行计算,同时满足数据共享安全和计算安全问题。而MKFHE可对不同公钥(用户)加密的密文进行任意计算,计算的结果由参与计算的用户联合所有密钥进行解密,解决了多用户密文进行同态计算的问题。另外在量子计算机时代下,在云计算服务场景中,有时需要将格上ABFHE技术与MKFHE技术结合,可在多用户环境下同时实现共享数据的细粒度访问控制和不同策略属性集密文的同态计算以及实现抗量子攻击能力。因此,如何实现更高效、更灵活的格上多策略属性基全同态加密方案是本课题的重点研究内容。
本文在第二章对本课题所涉及的相关背景知识进行了介绍。首先介绍了一些数学知识,如张量积、Garget矩阵和位分解、统计距离,然后介绍了格及相关概念,如格上困难问题、格陷门、离散高斯分布,其次介绍了伪随机函数,最后描述了ABFHE方案和MKFHE方案的形式化定义和安全模型。
本文在第三章提出了一个新的支持多跳的格上多策略属性基全同态加密方案,方案将单策略ABFHE与多跳MKFHE方案结合,方案的访问策略采用了任意多项式的布尔电路,实现了对数据的细粒度访问,并且方案实现了满足不同访问策略的不同属性集的密文之间进行全同态计算的功能,并具有更短的密文和更高的同态计算效率以及密文扩展更容易实现。此外,方案实现了多跳的功能,即同态计算过的密文能够与新加入密文再次进行同态计算,即使新加入密文所对应属性集不满足已有的访问策略集。最后证明了方案在LWE问题下是安全的。
参考文献(略)
