本文是一篇计算机论文,笔者针对现存的深度特征选择算法保留特征数目多且分类精度低问题,我们提出了基于提高癌症基因分类精度的两阶段深度特征选择算法TSDFS,它是一种高效的深度特征选择算法。
第1章绪论
1.1研究背景与意义
当今世界处于大数据时代,数据与人类如影随形。在大量的数据中,不仅存在对我们有益的数据,而且还有着毫不相关的垃圾数据,如何在包含巨量信息的数据中挖掘出对我们有益的数据或是能推动社会发展变得至关重要。在此背景下,特征选择(Feature Selection)技术应运而生。特征选择,它作为数据预处理一项至关重要的一步,在数据挖掘,模式识别和机器学习等方面有相当重要的作用[1]。选择数据中重要的特征,对提高计算效率具有重要意义。
现如今,在机器学习中具有代表性的特征选择算法并不少,例如根据与数据标签相关性可以将特征选择算法分为三个类型:(1)可监督特征选择算法;(2)半监督特征选择算法;(3)非监督特征选择算法。再者它又根据与学习器之间的关系将特征选择算法分为:(1)过滤式特征选择算法[1];(2)封装式特征选择算法[1];(3)嵌入式特征选择算法[1]。过滤式特征选择算法里面的方法主要是统计学方法,计算的是每个特征内部性能来判断这个特征的好坏,嵌入式和封装式特征选择算法考虑特征与学习器之间的关系,尤其是嵌入式特征选择更是根据学习器的性能来进行特征选择。封装式特征选择它是一种迭代特征选择算法,每次操作都要遍历一遍所有特征,所以该方法对于高维数据并不适用,具有较高的成本。然而,传统的特征选择算法对于当今高维数据已起不到很好地作用,因此,研究者们需要寻找出效果更好的选择特征的方法。
这些年来,深度学习的快速发展,很好地处理了如今数据维度过高的问题。深度学习从刚开始出现就受到广泛的关注,它的出现使各个领域都得到了更深层次的发展,像图像处理,语音识别,文本分析等领域都或多或少得到一定的发展。近些年来,研究者们将深度学习尝试应用到特征选择中构成深度特征选择算法也得到了良好的发展。深度学习可以提取特征中更深层次的表示也可以承担分类器工作,从而使特征选择得到更进一步的发展。最近有不少神经网络模型都应用在特征选择方法,像Taherkhani等人提出深度特征选择算法,使用受限玻尔兹曼机(RBM)对特征进行筛选[2]。
1.2国内外研究现状
随着信息时代的到来,各行各业产生的各种数据维度不断增加,人们都迫切希望从海量数据中选择出有用的信息。特征选择是从大量数据中选择重要信息的有效方法,它是数据预处理关键一步,在数据挖掘,机器学习等方面都有重要的作用。但现如今数据维度越来越高,传统的特征选择算法已达不到研究人员所需的要求,寻找更高效的方法迫在眉睫。深度学习的出现使得特征选择得到进一步发展,深度特征选择在图像处理,医疗处理方面有重要作用,尤其对于基因数据的选择方面有较强的发展前景。
随着微阵列技术的发展,近年来将深度特征选择算法应用在基因生物数据中已出现不少成果,像Kong和Yu在文献[8]中,作者在面对基因组数据特征远大于样本问题,提出了一种基于森林的深度学习算法(Forest Deep Neural Network,fD NN),使用随机森林进行特征选择对基因进行降维,之后使用DNN作为分类器查看效果。同年,两位研究者在文献[9]中又提出一种基于图嵌入的前馈神经网络(Graph Embedded Deep Feedforword Network,GEDFN),与传统网络不一样的是作者在输入层与第二个隐含层中嵌入了一个图矩阵,在特征空间进行降维操作。Shi等人提出DNP-AAP(Deep Neural Pursuit–Average Activation Potential)算法,进行抗菌素耐药遗传因子鉴定,DNP框架处理高维基因组数据和分类,嵌入AAP算法对特征重要性进行排序[10]。Ibrahim等人提出一种基于深度和主动学习的多层特征选择算法(Multilayer Learning Feature Selection,MLFS),使用深度置信网络(DeepBelief Network,DBN)作为特征选择框架,捕捉癌症基因的上层表示,之后通过无监督学习算法进行分类评估[11]。Koul等人提出一种基于交叉验证和无监督学习的特征选择策略确定癌症生物标记,使用递归特征消除进行特征选择,RF用来对选择后的基因进行五次交叉验证,最后使用DBN网络分类器对这些基因进行分类[12]。Syafiandini等人对直肠癌基因进行降维并查看分类精度,深度模型使用深度玻尔兹曼机(Depth Boltzmann Machine,DBM)对基因训练,测试,得到重构数据,根据重构数据与原始数据的均方误差(Mean Square Error,MSE)得到最优特征基因[13]。
第2章深度特征选择算法
2.1特征选择算法
特征选择目的是寻找一个低维空间,把高维数据映射到低维空间得到信息最大化表示,它的存在使快速分类高维数据成为可能。它根据特征选择过程和学习算法(这里的学习算法指的是机器学习中存在的分类算法或回归算法)的不同组合方式,将特征选择算法分为过滤式特征选择,封装式特征选择和嵌入式特征选择三种方式。其中,过滤式方法根据一些特征内在属性(如数据的信息内容)对单个特征或一组特征集进行排序,它根据数学统计学方面理论,把高维数据映射到低维空间。特征选择的封装式方法通过使用专属特征选择算法来评估基因的子集,并选择能产生最大分类精度的特征子集,它直接对特征集进行迭代操作选择出它认为当前最优的特征子集。嵌入式方法将特征选择作为模型预测的一部分,选择出的特征子集归功于特定的学习算法。下面详细介绍一下这三种特征选择方式。
2.1.1基本概念
(1)过滤式特征选择算法:过滤式的特征选择原理采用的是根据不同算法内部的评价标准,为每一个特征按照它对整体特征集合的贡献性进行打分,根据每个特征所得分数对特征进行降序排序,总的来说过滤式特征选择进行选择特征时进行的是统计学计算过程。符合该类型的特征选择算法在选择特征集之前,首先设置一个阈值,大于该阈值的所有特征被选出组成特征子集,低于该阈值的特征不被选择,没有被选择的特征集被淘汰删除。过滤式特征选择算法基本流程图如图2.1所示。

2.2深度学习算法
深度学习,作为机器学习的一部分将,它的出现计算机能够模拟人类大脑进行思考分析成为可能并且让数据分类得到质一般的发展。随着科技发展的越来越快速,深度学习也被应用到更多的领域。现如今,各行业都紧跟着大数据时代的发展,每个行业数据集都越来越庞大,但其中每种数据集包含的有用信息却很少,使用神经网络可以实现对数据集更深层次的提取。神经网络存在至今有两个主要的功能,其一是实现特征提取功能,去掉噪声、“垃圾”数据,得到更为干净的数据;其二是作为高效的分类执行者,提高数据分类精度。以上是神经网络模型存在的意义。对于深度特征选择算法的研究,神经网络模型更是不可缺少的一块,对于图像数据集,研究者们一般使用卷积神经网络(Convolutional Neural Networks,CNN)[31]来对图像进行逐层的处理,提取出图像具有代表性的信息,得到更好的分类性能。对于时间序列,研究者一般使用长短记忆神经网络(Long Short-TermMemory,LSTM)[32]进行深层提取,因为LSTM中包含记忆元对处理时间序列具有重要意义。而我们所要研究的生物数据集,大多数为矩阵组成的一维序列数据,研究者们一般都是用自编码器(Autoencoder,AE)[33]或者受限玻尔兹曼(RestrictedBoltzmann Machine,RBM)[34]对其进行提取特征获得特征表示,下面主要对自编码器衍生出的变分编码器进行介绍。
(1)AE模型
自编码器是一种基于无监督的神经网络的学习算法,它通过反向传播技术设置使得神经元输出节点数与输入节点数相等。研究者们喜欢使用自编码器主要目的有两种分别为:1)去噪,如今数据集越来越多,里面包含的垃圾也越来越多,通过去噪可以得到更干净的数据集;2)降维并且可视化,自编码器在有条件要求下,它可以在神经网络中可以当做一个降维学习器,它就类似于机器学习中的代表算法主成分分析(Principal Component Analysis,PCA)[35],可以实现对高维数据集进行降维并通过一定的方法可以查看降维后的节点分布情况,降维与特征选择定义相似但不相同,特征选择是进行物理选择结果保留特征本身内容,降维则是对特征内部信息进行操作,提取特征中潜在的信息,得到特征中的表示,从而实现降低特征维度,提高计算能力和精度。自编码器是一种无监督式的神经网络模型,它本身包括两个阶段分别为编码(encode)阶段和解码(decode)阶段。自编码工作流程为将原始数据特征构造成输入节点导入自编码器的输入层,经过编码阶段,去除特征中包含的噪声并提取特征中的表示,得到的低于输入层节点的数目,降低维度,实现去噪和降维操作,之后得到降维后的数据通过解码阶段,对降维后的特征数据集进行数据重构,进而得到与输入层节点数相同的特征数,需要注意的是经过自编码操作后的特征集和最初输入的特征集相似但不相同,原因为操作后的特征集即使节点数是相同的但是却不包含最初特征内部的噪声。因此自编码器操作的最终结果是获得了富含信息量更多的特征数据。
第3章基于两阶段深度特征选择算法........................19
3.1 TSDFS算法.......................................19
3.1.1集成特征选择..........................................20
3.1.2变分自编码器特征提取............................21
第4章基于随机森林的深度特征选择算法............................39
4.1概述.......................................39
4.2基于随机森林的深度特征选择算法.....................40
4.2.1随机森林特征选择过程.............................41
4.2.2基于神经网络学习分类特征.......................41
第5章总结及下一步研究工作................................59
5.1总结.................................59
5.2下一步研究工作...............................60
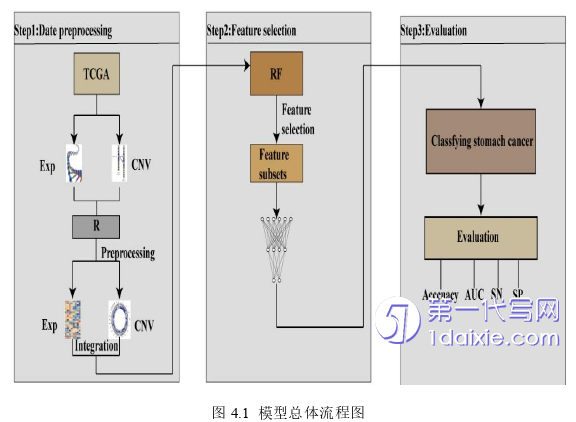
第4章基于随机森林的深度特征选择算法
4.1概述
随着生物数据的不断增多,研究者们发现只考虑一种类型的基因数据来进行癌症分析已得不到好的结果。因此现在多数研究者都开始研究整合多类基因组数据来进行特征选择,提高癌症的预测精度,人类全基因组数据包含有多种类型基因,它们另称为组学数据,因此整合多类基因组数据也称整合多组学数据。本章针对整合胃癌多组学数据进行深度特征选择来提高胃癌组数据的分类精度。胃癌仍是世界上最致命的肿瘤之一,且多数患者5年生存率为25%[54]。一旦扩散到腹膜,生存率下降到5%[55]。胃癌多数患者无明显症状,少数人恶心,呕吐或类似于溃疡病的上消化道症状,所以难以引起足够的重视。然而,高达40%胃癌患者在病程期间会发生一定的腹膜转移[55],因此设计有效的方法来提高胃癌的预测精度极其重要。
近些年来,高通量技术的发展为获取不同类型的全基因组多组学数据提供了具有成本效益的方法[20]。例如癌症基因图谱(TCGA)正在收集肿瘤的多组学数据和临床数据[56]。TCGA隶属于美国健康研究院(National Institutes of Health,NIH)的美国国家癌症研究所(National Cancer Institute,NCI)和国家人类基因组研究所(National Human Genome Research Institute,NHGRI),它收录了许多癌症基因数据,包括基因表达数据(Exp)(转录组学数据),拷贝数变异数据(CNV),蛋白质表达数据,体细胞突变数据(SNV),甲基化数据等[56]。生物基因数据大多具有高噪声,多元高维和多元异质的特性,生物基因组数据很多特征是和表型不相关的,特征之间也存在着冗余,且高通量技术产出的生物基因特征大多数也存在“大p小n”的维度灾难问题,“p”指的是特征数量,“n”指的是样本数量。因此,特征选择是克服高维基因数据维度灾难问题的有效方法。特征选择方法在生物信息学领域被广泛的应用于识别生物标志物和数据降维。特征选择方法的主要优点是它保留了原始特征集合的物理含义并且提供了更好的模型可读性与可解释性,得益于这一优点,特征选择方法没有更改原始数据的特征空间,在生物信息学领域有助于进一步分析所选特征的生物学功能[57]。
第5章总结及下一步研究工作
5.1总结
本文针对当前存在的深度特征选择算法处理基因数据分类效果不高问题,提出了两种不同的深度特征选择算法,两种算法改进了已存在的深度特征选择算法的缺陷并大大提高了分类和计算效率。
(1)绪论系统的介绍了特征选择算法和深度学习概念并引出了面向基因数据深度特征选择算法的发展及其国内外发展现状,并展示了现存的深度特征选择算法处理基因数据存在的问题,同时本文的研究内容及贡献做了概括说明。
(2)介绍了典型的特征选择算法和神经网络模型,进而介绍了近几年研究者提出的深度特征选择算法。
(3)针对现存的深度特征选择算法保留特征数目多且分类精度低问题,我们提出了基于提高癌症基因分类精度的两阶段深度特征选择算法TSDFS,它是一种高效的深度特征选择算法。为了解决其他算法保留特征数量多的问题,TSDFS算法中包含一集成特征选择过程,通过不同方面进行特征选择,大大减少了特征数量;并且为了提高特征分类精度我们使用VAE模型对集成特征选择过程中产生特征子集进行特征提取,得到特征子集的最佳表示。经过大量的实验结果证明TSDFS算法能有效的提高分类效率和计算速度,而且也证明了在特征选择方面可以选择出具有重要意义的基因特征。
(4)目前在面向基因数据进行深度特征选择大多数使用的都是单一层面上的基因数据,并没有考虑整合不同层面的基因数据来提高癌症的预测分类精度。为了解决上述问题,本文提出了一种基于胃癌多基因组的深度特征选择算法RDFS。该算法中通过随机森林RF来进行特征选择,选择出特征重要性较高的特征组成特征子集,之后将特征子集导入神经网络中,通过层层操作,进而提高分类预测精度。并且最终通过大量实验证明,RDFS算法可以明显的提高胃癌多基因组数据的分类精度且选择出的特征也具有重要的研究价值。
参考文献(略)
