本文是一篇计算机论文,本论文开始介绍了选题背景及意义,还介绍了与图像预处理的量子图像二值化算法和图像实际操作的量子图像二值形态学边缘检测算法相关研究的研究发展现状,包括量子图像表示方法、量子图像二值化算法和量子图像边缘检测算法。
第一章 绪论
1.1 选题研究背景及意义
量子计算是一种将经典计算机信息理论与量子力学理论相结合的迅速发展的新兴技术,是一种富有洞察力的信息计算范式[1]。量子计算利用量子叠加特性,量子纠缠特性和量子相干特性实现量子系统的并行计算,量子计算的并行运算能力无疑是未来计算的一部分[2]。 20 世纪 80 年代,理查德·费曼对通用量子模拟器的概念进行了探讨,即一台可以利用量子效应探索其他量子效应并运行模拟的机器量子力学模拟器的计算机,通过理论证明,量子计算机是可实现的。在20世纪90年代由DR Jozsa提出的用于解决特定问题的Deutsch-Jozsa 算法[3]和Grover提出的一种快速数据库搜索的量子力学算法(也称Grover算法)[4],更是证明了量子计算机的加速计算的优势,也使得越来越多的研究者对量子计算机方面的各种技术和应用进行了深入的研究,量子图像处理作为其中一项也得到了较多研究者们的青睐。
视觉是人类最直接和普遍常用的感知,在人类认知自身及周围环境时起着主导的感知作用。由于主要采用视觉对世界进行感知,人们得到的感知信息是由图像的方式呈现出来的,因此,图像在人类探知世界的活动中有着极为关键的作用。图像处理不仅包括输入和输出都是图像的处理,也包括从图像中提取特征的过程[5]。图像处理领域的图像来源包括人类视觉角度产生的图像和成像机器视觉角度产生的图像,因此图像处理技术也涵盖了非常宽的不同应用领域,比如机器人视觉方面[6,7,8]、图像编码通信工程[9,10,11]和生物医学分析处理方面[12,13,14]等,也可以说图像处理在各个领域都有着重要的作用。
量子计算机的量子化存储读取、量子通信安全性极高和数据处理并行计算使得量子计算机具有独特的优越性质[15]。量子图像处理是量子信息处理的一个分支,致力于将传统的数字图像处理算法转换为在量子计算环境下的量子图像处理算法,从而提高复杂图像处理算法的效率。在量子计算的研究方向中,研究者们对量子图像处理聚焦了极大的关注,许多研究人员对量子图像处理进行探索研究工作以优化各种图像处理算法的快速性、高效性和准确性。
1.2 国内外研究现状
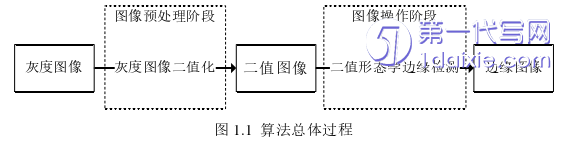
本文研究了图像二值形态学边缘检测算法的总体过程量子设计与仿真,其中包括了图像预处理阶段的量子图像二值化算法和图像操作阶段的量子图像边缘检测算法,一个有效的量子状态制备方案是许多量子图像处理算法的先决条件,因此这两个算法都采用NEQR模型量子图像表示方法对图像进行量子图像状态制备。量子图像表示方法、量子图像二值化算法和量子图像边缘检测算法目前的研究发展如下。
1.2.1 量子图像表示方法
在量子图像处理领域,量子图像表示方法是研究量子图像处理的首要工作[28,29]。在2005年,S.E.Venegas等开发了一种在量子力学系统中存储和检索二值图像的新方法[30],通过使用非纠缠和纠缠量子位存储和检索图像的方法,将二值图像信息存储在量子系统中,利用量子计算的思想开发图像处理算法。目前,在量子图像处理领域普遍使用的量子图像表示方法是 FRQI模型(Flexible Representation of Quantum Images) [31]和NEQR模型(A Novel Enhanced Quantum Image Representation) [32]。FRQI模型是由Le等在2011年提出,为多项式制备过程和基于酉算子的量子图像处理操作提供了基础,将数字图像中每个像素的像素信息和位置信息以归一化的数学形式存储为量子叠加状态,为量子计算机上的图像提供了一种存储表示方法,在利用量子叠加态的优势下,FRQI模型用 2n+1个量子比特位就可以存储表示大小为2n×2n的数字图像。在 FRQI 模型的基础上,Zhang等在2013年提出了NEQR模型量子图像表示方法,NEQR 模型保留了 FRQI 模型图像位置信息的表示方法,改进了 FRQI 模型的像素信息表示方法,用q个量子比特的基态来存储图像中每个像素的灰度值信息,因此NEQR模型使用 2n+q 个量子比特位就可以存储表示大小为2n×2n,灰度值范围为[0,2q−1]的数字图像,因此NEQR模型量子图像表示方法可以对所存储的图像灰度值进行相关操作,相比于其他的量子图像模型更灵活且更适用于量子图像处理算法的研究。
第二章 基础知识及相关概念
2.1 量子比特
量子比特,又称量子位,是量子信息的物理载体[47,48]。它是经典比特的量子版本,正如经典比特有两种状态0和1,量子比特也有两个基本的正交基态|0⟩和|1⟩,| ⟩这样的符号被称为狄拉克符号[49],在量子计算机中是表示量子比特状态的标准符号。
Toffoli门和n-CNOT门的具体逻辑操作与CNOT门的具体逻辑操作一脉相承,作为控制目标的量子比特的数量恒定为1,具体的区别在于:CNOT门是一个条件双量子比特门,作为控制条件的量子比特的数量是1;Toffoli门是一个条件三量子比特门,作为控制条件的量子比特的数量是2;n-CNOT门是一个条件n+1量子比特门,作为控制条件的量子比特的数量是n。应用Toffoli门和n-CNOT门时,只有当Toffoli门和n-CNOT门作为控制条件的量子比特的状态都为|1⟩态时,作为控制目标的量子比特会如同应用了非门一样翻转量子比特的状态;否则,作为控制目标的量子比特的状态不会改变。在Toffoli门和n-CNOT门中,只有作为控制目标的量子比特的状态会根据作为控制条件的量子比特的状态进行相应的变换,作为控制条件的量子比特的状态是一直保持不变的。
2.2量子比较器
量子比较器、量子加法器和量子减法器等基本量子模块电路是实现量子处理算法的重要基础。量子比较器与数值比较器有些相似,都能比较两个二进制数的大小的不同,但量子比较器是用于量子计算机中的量子比特,所以量子比较器比较的是两个量子逻辑状态的大小。在整个量子电路中,量子电路的线路复杂度越低效果越好,在量子计算模拟系统中仿真便更容易实现。但是目前的量子比较器大都要求较多的辅助量子比特,电路操作较复杂,这就导致了整个量子电路的构造代价较为高昂,也极大的增加了量子电路的线路复杂度,使得难以在量子计算模拟系统中仿真实现。因此,选择的量子比较器所要求的辅助量子比特越少,整个量子比较器电路的使用的量子比特就会越少,在量子计算机中量子运算的代价就会更低,在量子计算模拟系统中就更容易仿真实现。
张等利用波纹携带思想,提出了一种仅需要一个辅助位就可以实现两个n位量子逻辑状态的量子比较器[55]。假设需要比较的两个量子逻辑状态数为|𝐴⟩和|𝐵⟩,都由n个量子比特表示,|𝐴⟩表示为|𝐴𝑛−1𝐴𝑛−2...𝐴1𝐴0⟩,|𝐵⟩表示为|𝐵𝑛−1𝐵𝑛−2...𝐵1𝐵0⟩,其中|𝐴0⟩和|𝐵0⟩均为最低量子比特位。对于这两个量子逻辑状态数为|𝐴⟩和|𝐵⟩,该量子比较器运用波纹携带的思想,设计了基本的波纹携带门,先实现最低量子比特位|𝐴0⟩和|𝐵0⟩的大小比较,携带量子比特可以携带最低量子比特位的量子态的减法借位信息进一步实现量子态|𝐴1𝐴0⟩和|𝐵1𝐵0⟩的大小比较,这样可以在不增加辅助位的情况下,从最低位到最高位进行逐位比较,从而实现n 位量子序列数|𝐴⟩和|𝐵⟩的比较。
第三章 基于IBM Q的量子图像二值化算法 ....................... 18
3.1 量子灰度图像表示 ............................................. 18
3.2 量子图像二值化算法设计 ............................. 19
第四章 基于IBM Q的量子图像二值形态学边缘检测算法 .................................. 31
4.1 量子二值图像表示 ....................................... 31
4.2 量子图像二值形态学边缘检测算法设计 ............................. 32
第五章 总结与展望 ................................ 44
5.1 论文工作总结 ..................................... 44
5.2 优缺点与展望 ............................... 45
第四章 基于IBM Q的量子图像二值形态学边缘检测算法
4.1 量子二值图像表示
本章所设计的二值形态学的量子图像边缘检测算法初始的量子图像表示采用了2.32节中的NEQR量子二值图像表示,将数字二值图像转换表示为正常的NEQR量子二值图像表示,以满足算法中量子循环移位变换操作的量子图像表示需求。
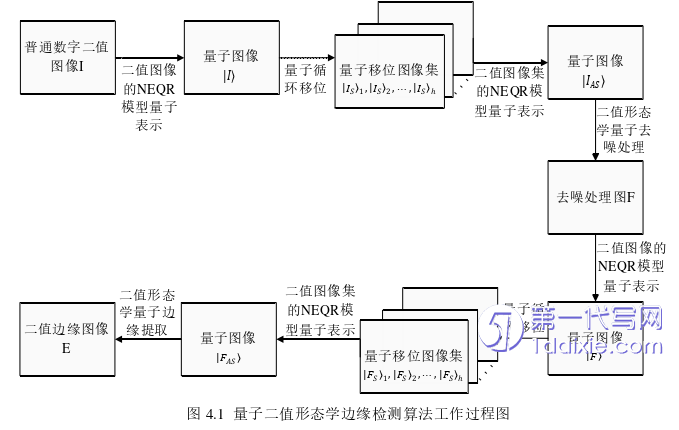
本节在2.5节提到的量子二值腐蚀与膨胀操作的基础上,进一步设计了二值形态学量子图像去噪处理和二值形态学量子图像边缘提取两个量子电路,二值形态学量子图像去噪处理和二值形态学量子图像边缘提取两个量子电路共同组成了本章所设计的量子图像二值形态学边缘检测算法。
量子二值形态学边缘检测工作过程如图4.1所示。
第五章 总结与展望
5.1 论文工作总结
由于量子图像处理是一个新兴事物,关注与研究它的研究人员不仅会面临巨大的机遇,也会面临许多量子方面的挑战。本文旨在研究整个量子图像二值形态学边缘检测算法的总体流程,结合IBM Q平台设计与图像预处理阶段的量子图像二值化算法和图像操作阶段的量子图像二值形态学边缘检测算法相应的量子电路以及实现这两个算法的量子仿真,论文具体工作总结如下:
(1)论文开始介绍了选题背景及意义,还介绍了与图像预处理的量子图像二值化算法和图像实际操作的量子图像二值形态学边缘检测算法相关研究的研究发展现状,包括量子图像表示方法、量子图像二值化算法和量子图像边缘检测算法。从量子比特状态的三种量子线性表示的概念入手,介绍量子计算中的基础知识和与论文相关的基础知识与相关概念,对基础量子门的电路表示、数学矩阵表示和具体状态作用效果进行了具体的介绍,包括单量子比特门和多量子比特门。从数学量子表达式和量子电路实现图的角度,详细介绍了NEQR量子图像表示方法、量子二值腐蚀与膨胀操作和量子循环移位变换的相关概念,最后介绍了IBM Q平台的量子仿真方式和具体信息。
(2)针对目前对于量子图像二值化算法的研究较少的问题,提出了一种易于实现、电路线路简单的基于IBM Q的量子图像二值化算法。这个基于IBM Q的量子图像二值化算法先结合量子图像二值化算法的输入需求改进了NEQR量子灰度图像表示方法,随后对现有的波纹携带量子比较器的一个基础波纹携带门在IBM Q平台上进行了适应性表示与电路精简优化,根据适应性表示与电路精简优化之后的基本波纹携带门设计了一个只需一个辅助量子位的量子比较器电路,然后通过这个量子电路设计实现了基于IBM Q的量子图像二值化算法,整个算法只需要一位辅助量子位,大幅降低了算法量子电路的复杂性,使算法的量子电路易于实现。最后在IBM Q平台上对量子图像二值化算法进行了仿真实现与复杂度分析,论证了这个量子图像二值化算法的正确性、有效性和优越性。
参考文献(略)
