本文是一篇计算机论文,本文主要针对正负反馈WTA模型收敛速度慢,抗干扰性能差的问题,提出一种改进的正负反馈WTA模型。该模型采用1-范数来统计全局状态变量,由符号函数来提供状态变量的正负反馈。
第一章 绪论
1.1 课题研究背景及其意义
竞争与合作广泛存在于生活当中,从达尔文的生物进化论开始,动物间弱肉强食,适者生存就从来没有停息过。到现在正在进行的俄罗斯与乌克兰的战争,以及上世纪美苏之间的冷战,都表现了竞争的普遍性。不同的竞争方式,或者说竞争导致的结果是不同的。有的情况下,竞争可以实现双赢,比如两个学生比赛谁的期末成绩更好,经过努力的学习,两人大概率都能取得好成绩,实现双赢的结果。但是,很多时候,竞争都是会有赢家和输家,输家不止一个,赢家也可能有一个或者多个。赢者通吃(winner -take -all WTA)竞争,在竞争中只有一个胜利者,胜利者拿走所有的资源,并打压其他失败者的发展,这种竞争的方式比较特别。秦始皇统一六国,也是由于秦国的强大,在与六国的竞争当中获胜,把六国的所有疆土据为己有,这才有了吞并六国后的秦国疆土。这也是一个赢家获胜,得到所有的可用资源的例子。相对来说,这种赢者通吃是比较残酷的,失败方会苦不堪言。现如今,随着互联网的发展,人工智能深入生活的方方面面,大家所关注的赢者通吃的行为已经不止局限于宏观世界,而更多的向微观世界探索。赢者通吃的竞争也已经受到了越来越多研究学者的关注。
赢者通吃在多机器人控制,神经网络,深度学习,生物计算等方面得到了广泛关注,本课题也来源于此。研究人员尝试设计非常多复杂的模型去模拟这种赢者通吃现象,这些模型被用来解决硬件设计问题,凸二次规划问题,控制领域问题等,并在这些问题上取得了较大的发展。例如,赢者通吃的L-volterra模型模拟了自然界的竞争,猎豹和鹿之间只有不断提高奔跑速度才能存活下来 [1]。在神经计算方面,人类大脑里的神经竞争采用交互式的F-Nagumo模型来模拟 [2]。在植物竞争方面,对于大多数的植物而言,在其发育的初始阶段,主茎稍微比其他的侧茎生长的更强一点,在其今后的生长中将会越来越强,并最终占据主导地位[3]。在社会当中,一些企业一旦取得成功,随着时间一天天过去,这个企业可能会发展的越来越好,而其它与它同类型的企业则会渐渐的落后于它,这在现在的互联网行业表现的特别明显[4]。赢者通吃竞争的发展,在很多领域做出了不可磨灭的贡献。
1.2 研究历史及现状
赢者通吃是一种在生活中广泛存在的普遍现象,国内以及国外的非常多的科研人员对其进行了大量的研究,其中的研究领域包括生物科学领域、神经网络领域、电路控制领域、机器人控制领域等。这一小节将选取一些比较有代表性的研究领域加以阐述。其中,神经网络计算领域的研究代表性较强,机器人、无人机、机械手等群体领域的研究也比较值得探讨。在动态控制系统中所谓的赢者通吃,指的是由代理人通过相互竞争激活的方式,仅由输入信息较多,或者投入资源较大的代理人处于激活状态,其他代理人都被抑制。这一小节,将阐述赢者通吃的研究历程及其研究现状。
1.2.1 赢者通吃在神经网络方面的研究
许多赢者通吃模型的计算原理同神经网络的计算原理非常类似,很多情况下可以将赢者通吃的计算当作神经网络计算的一种特例,可以把赢者通吃模型的节点视作为一个个神经元。传统结构里,赢者通吃中的各个神经元在迭代的过程中,具有最大激活量的神经元保持活跃状态,剩下不是最大的神经元的活动受到抑制。对原有计算的结果进行扩展,如果最后的结果不止一个而是多个神经元被激活,这样称为多赢者通吃的竞争。因为神经网络中神经元的总数和硬件网络实现的复杂度以及生产成本相关,而赢者通吃神经网络中的神经元总量相对较小,因此一些研究者尝试用硬件电路来实现赢者通吃网络[11]。并且研究人员也已经提出了各种类型的模型来模拟产生赢者通吃现象,比如已经提到的n维的L-Volterra模型来模拟n维物种的竞争[1]。近些年,递归神经网络发展迅速[12,13],许多科研工作者也已经开始使用递归神经网络来解释赢者通吃的竞争[14,15],比如严格的理论证明了交互式F-Nagumo模型来产生赢者通吃现象[16]。赢者通吃问题还可以作为一种优化问题的更加合适的解决方案[17]。不仅如此,在高速并行计算方面,神经网络表现强劲,它由硬件来实现,在实时性要求高的系统中得到应用广泛,比如动态神经网络用于多无人机的合作以及冗余机器臂的任务分配等[18]。
第二章 相关模型和背景知识介绍
2.1 引言
赢者通吃(winner-take-all,WTA)的竞争在自然界中广泛存在,并且已经应用到了许多工程领域。赢者通吃是指对于一组参与竞争的竞争个体或者说代理,优势最大的代理获得胜利,通吃全部资源,而失败者什么都没有。研究人员提出了许多复杂的数学模型来模拟这种现象,并将这些模型应用到了机器人控制、深度学习、硬件电路等等领域。本章对一些经典的赢者通吃模型进行介绍,其中包括正负反馈的赢者通吃模型。后面章节将基于正负反馈赢者通吃模型来进行改进及应用。
2.2 赢者通吃模型介绍
2.2.1 离散型赢者通吃模型
这一节介绍一种离散的WTA模型[76],该模型以一种简单的线性差分方程来模拟赢者通吃现象。模型首先由向量进行输入,然后经过不断的迭代,选择出具有最大输入的元素。
2.2.2 正负反馈赢者通吃模型
这一节介绍具有正负反馈的WTA模型[27],这种类型的的竞争模型是从整体出发,从整体到局部再到个体。对于在系统中的每个竞争的个体而言,其初始值在经过不断的迭代之后而趋于稳定状态,在稳定状态下的输出即为整个系统的解。具有最大输入的个体经过不断迭代,其值在迭代中不断增加,最后趋于稳定状态而获胜。其他非最大输入的个体,其值在迭代不断受到抑制,最后趋于0的稳态。
2.2.3 分布式的赢者通吃模型
在这一部分,通过提出一种分布式的WTA模型[28]来解决连通图上的分布式WTA问题。分布式WTA问题通过个体之间的相互作用提取出全局的竞争动态,因为在网络上全局最大值的目标与局部节点领域的可访问信息之间需要进行对比,这实际上是一个非常具有挑战性的问题。它与另一个具有挑战性的问题使用局部信息来搜索多峰函数的全局最大值比较相似。与作为分布式计算的强大工具而在过去几年被广泛研究的动态共识协议相比,WTA走向了共识的另一个极端,增加了分歧。对于共识问题,包括平均共识、加权平均共识甚至最大共识,不同节点的不一致随着时间的推移进而减小为零。与此相反,对于WTA问题,赢家的节点保持活跃状态,而输家的节点被抑制为零,这相当于增加了赢家和输家之间的分歧。虽然有各种各样的WTA模型,但它们都依赖其他节点,而不是其直接邻居节点来获得每个代理的状态更新信息。
第三章 改进的正负反馈赢者通吃模型 ................................ 15
3.1 引言 ............................ 15
3.2 改进的正负反馈赢者通吃模型 .............................. 15
第四章 多足球机器人目标轨迹跟踪与协调竞争的控制策略研究 ......................... 27
4.1 引言 ....................................... 27
4.2 足球机器人的目标轨迹跟踪 ................................ 27
第五章 总结与展望 ........................................... 40
5.1 本文工作总结 ....................................... 40
5.2 研究展望 .............................................. 41
第四章 多足球机器人目标轨迹跟踪与协调竞争的控制策略研究
4.1 引言
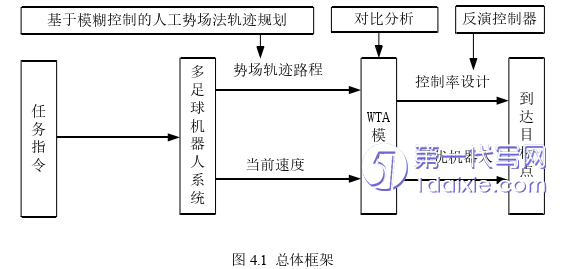
本章节采用改进的WTA模型对多足球机器人之间的抢球竞争进行决策,与前人采用的方法相比,采用改进的WTA模型收敛的速度更快,机器人的运动更加平稳。在多足球机器人系统中,如果所有机器人都去争抢一个足球,必然会造成能量的巨大浪费,那么决策出一个最优的足球机器人去抢球是需要考虑的一个问题。本文针对多足球机器人系统中的抢球问题,提出一种基于改进的赢者通吃(WTA)的最优控制策略。该策略先使多足球机器人系统的每个成员与目标之间通过结合模糊控制的人工势场法各自生成一条理想的避障轨迹,计算每条轨迹到达目标点的路程。然后与该机器人的当前速度结合,输入到改进的WTA控制模型,决策一个最优的机器人赢得竞争执行此任务。最后获胜的足球机器人根据设计的控制率,沿着理想轨迹到达目标点。机器人到达目标点的理想轨迹通过人工势场法生成,传统的人工势场法容易陷入局部极小值的问题,结合机器人的实际情况,将人工势场与模糊控制相结合,避免了局部极小值问题,顺利实现理想轨迹的跟踪。图4.1为本章的总体框架。
第五章 总结与展望
5.1 本文工作总结
赢者通吃的竞争在自然界和社会中广泛存在,同时在许多的工程领域得到了应用,比如机器人控制领域、生物神经元领域、深度学习领域、硬件电路领域等,也一直受到了研究学者的广泛关注。本文基于正负反馈赢者通吃模型提出了一种改进的赢者通吃模型来产生赢者通吃的竞争。对改进的模型进行了各种仿真,并将该模型应用于足球机器人抢球问题。后面对本文工作做主要总结。
(1)主要针对正负反馈WTA模型收敛速度慢,抗干扰性能差的问题,提出一种改进的正负反馈WTA模型。该模型采用1-范数来统计全局状态变量,由符号函数来提供状态变量的正负反馈。与原模型相比,采用1-范数的改进模型降低了统计量的计算复杂度,提升了模型的收敛速度。由符号函数提供正负反馈,降低了噪声对模型的干扰,提升了模型的抗干扰性能。通过与原模型的对比仿真实验,验证了改进的WTA模型相比于原模型具有更快的收敛速度。增加高斯白噪声的干扰实验,验证了改进的模型相比于原模型具有更强的抗干扰性能。接下来对提出的改进模型的稳定性进行了严谨的数学证明,同时也证明了改进模型最终收敛的平衡点。接下来通过仿真实验来验证数学证明的结果,实验结果完全符合数学证明的结论。对改进WTA模型的局部稳定性进行实验分析,结果表明,除理论证明的稳定的平衡点外,其他所有的平衡点都是不稳定的。随意对这些不稳定的平衡点加一个很小的扰动,都能打破平衡状态,收敛到理论证明的稳定的平衡点处。最后对改进的WTA模型进行动态竞争仿真,实验结果也表明了改进的WTA模型同样适用于动态竞争场景。
(2)将改进的赢者通吃模型应用到多足球机器人抢球竞争。针对多足球机器人抢球问题,提出一种基于改进的赢者通吃模型的最优控制策略。该策略先使多足球机器人系统的每个成员与目标点之间通过模糊控制人工势场法各自生成一条理想的避障轨迹,计算每条轨迹到达目标点的路程。将路程与机器人的速度输入到改进的WTA模型,决策一个最优的机器人赢得此抢球任务。与前人采用原正负反馈WTA模型解决此问题进行对比,采用改进模型的机器人反应速度更快,能更快的到达目标点。足球机器人抢球过程中可能存在各种噪声的情况,本文还进行了抗噪声干扰的实验,实验表明改进的WTA模型应用在抢球竞争时对噪声的干扰不敏感,能够稳定的收敛。后面还进行了动态仿真实验,在球和机器人都是随时间变化的情况下,改进的WTA模型仍能够实时地找到胜利者。
参考文献(略)
