本文是一篇计算机论文,本文为探究天牛群优化算法在实际工程应用中的表现,文中在算法的个体位置表示上进行改进,提出了离散天牛群优化算法,并应用于卫星导航的选星问题。
第1章 绪论
1.1 研究背景
随着人类社会的不断发展和改造世界步伐的加快,工作和生活中会出现各种的优化问题。例如:机器人在执行某一任务时,需要它通过某一段路,此刻需要在众多的可能路径中选择出来一条,既希望它尽可能快地完成任务,又希望机器人在执行任务的过程中花费的能量尽可能的少;再比如病人查出疾病后,医生选择病人的治疗方案,多久做一次治疗?治疗的时候使用的药品剂量为多少?如何降低治疗造成的副作用?其中的抉择还取决于病人的年龄段,疾病的位置,疾病的类型,病人的整体身体状况等因素。以上两个在连续的变量区间中寻找最优解的例子,称其为函数优化问题。而如果问题中的变量是离散型的,则又称该问题为组合优化问题,典型的代表有:旅行商问题、图着色问题、装箱问题、0-1背包问题和生产调度问题等。
在工程设计领域中,最优化问题的表现形式为寻找一组参数,在满足一系列的相关限制约束下,要使得目标函数达到最优值。因此,最优化问题的三要素分别为决策变量、约束条件和目标函数。对于最优化问题又可分为单目标优化问题和多目标优化问题,相对于单目标优化问题,多目标优化的本质是不存在唯一的全局最优解。因为后者存在多个目标函数,而这些目标函数之间是相互制约的关系,一个目标的改善可能会引起另外一个或是多个目标的性能降低,因此想要使得所有的目标函数达到最优结果是不可能的,而只能是不断协调,从而找出一个使得所有目标函数尽可能达到最优化的解。
随着计算机的不断发展,它可以代替人类高效地完成一些需要大量计算与逻辑处理的工作,比如计算弹道导弹的运行轨迹等。但当人类想要进一步发展人工智能,使得计算机也可以完成一些人类擅长的事情,比如人脸识别和语音识别时。人类开始尝试从生物的行为中获得启发,进而便有了神经网络、模糊系统、遗传算法以及其它多种多样的智能优化算法的产生。
1.2 研究意义
在面对有较为明确的问题和条件描述的结构化问题时,此时最优解一般是确定的,表现为单峰现象,使用传统的优化算法便可以得到一个较为满意的结果。该类算法经历的过程包括:确定初始方案,依据严格的数学原理对初始的方案进行一定次数迭代,最后得到最终方案。但是对初始方案的依赖性决定了得到的最终方案可能会出现极好或者极坏的极端现象;其次,该类算法一般需要提供梯度信息,会增加算法求解的复杂度。智能优化算法依靠其简单的规则和随机性可以实现一定变量范围内的多峰极值问题求解,而算法的原理多是来自于自然界中的现象或过程。对初始方案的弱依赖性以及不需要提供梯度信息方面成功地弥补了传统优化算法的不足,并为解决复杂优化问题提供了一种全新的解决方法。因智能优化算法具备强寻优能力和有效避免陷入局部最优解的优势,使得该类算法被广泛运用到不同领域中,并吸引了众多学者对其进行研究,其有效性也在大量的应用论文中得到了证实。
最早提出也是最著名的智能优化算法便是70年代提出的遗传算法[1],其通过模拟自然界生物的生存和进化,对问题解采用概率化进行随机搜索。遗传算法一开始为了研究自适应系统和自然选择的过程,而后经过不断的发展,因其优秀的寻优性能,被广泛的运用到各种领域中,包括函数优化[2]、资源分配[3]、系统优化[4]和路径优化[5]等。众多研究学者认定其存在具有巨大的研究价值,纷纷投入到该方向的研究中,随后越来越多的智能优化算法被提出,如模拟鸟群觅食的粒子群优化算法[6]、源于蚂蚁觅食时释放信息素行为的蚁群优化算法[7]、以化学物质的冷却和结晶为基础的模拟退火算法[8]等。
第2章 相关研究
2.1 智能优化算法
智能优化算法作为进化计算的一个活跃分支,隶属于计算智能的范畴,而其中提及的“进化”概念多指算法通过多次的迭代使得解得到优化的过程。依据搜索问题解所需使用的个体数,智能优化算法可分为单体智能优化算法和群体智能优化算法,相较于前者,群体智能优化算法更适合应用于求解高维情况下的复杂优化问题。
群体智能的概念最早是由Beni等人[31]在1989年的文章“Swarm Intelligence in Cellular Robotic Systems”中提出的。群体智能优化算法具备参数少,模型简单,易于实现和容易相互融合改进等优点。在算法原理上,它们具有一定的共性,即由组成群体的多个个体之间相互协作,具备直接或间接地相互传递信息,并交互式地适应环境的能力,使得群体中的个体对环境的适应性越来越好,从而逐渐求得偏近问题全局最优解的足够好的近似解[75]。智能优化算法依靠其在求解复杂问题和优化问题上的明显优势,使其成为目前的研究热点。接下来,本章接下来将介绍一些较常见的群体智能优化算法,并在下一节对天牛群优化算法进行详细的介绍。
遗传算法(Genetic Algorithm, GA)由Holland等人[1]在1971年提出,起初源于对生物系统的计算机模拟研究,后来受到启发而创造出了一种基于生物和进化机制的自适应概率优化技术,即遗传算法。该算法使用带有固定长度的二进制符号串来表示种群中的个体,依据适应度函数的值来判断个体的优劣,并通过选择、交叉和变异这三种算子来模拟生物进化过程中个体优胜劣汰、基因重组和基因变异的演化过程。GA具有快捷,简便和容错性强的特点,为复杂系统优化计算问题提供了一种新的解决方案。
2.2 天牛群优化算法
2.2.1 天牛须搜索算法的基本原理
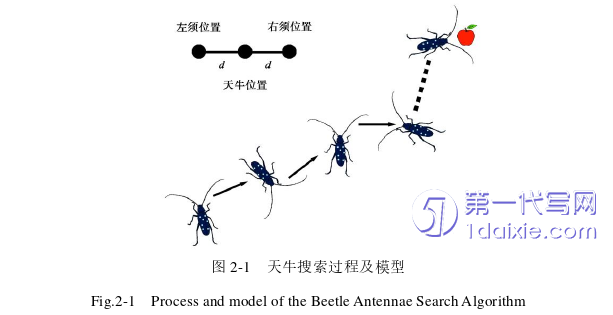
在自然界中,天牛个体在觅食过程中会通过头顶的两根触须检测周围食物的信号浓度,并向高浓度的一侧进行移动。天牛须搜索算法的提出便是基于此现象,天牛个体觅食的过程以及抽象出的简易模型如图2-1所示:
第3章 基于权值分配策略的聚类天牛群优化算法 ..................... 13
3.1 改进算法基本原理 ........................................... 13
3.2 基于权值分配策略的聚类天牛群优化算法 .......................... 14
第4章 带Tent映射的云模型天牛群优化算法 ................................. 25
4.1 改进算法基本原理 ............................................. 25
4.2 带Tent映射的云模型天牛群优化算法 .................... 28
第5章 基于离散天牛群优化算法的导航选星方法 ..................................... 39
5.1 导航选星问题 ........................................... 39
5.2 基于离散天牛群优化算法的导航选星方法 .................................... 42
第5章 基于离散天牛群优化算法的导航选星方法
5.1 导航选星问题
5.1.1 引言
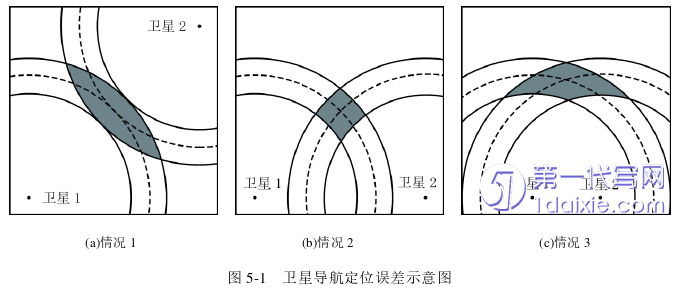
近些年,随着全球导航卫星系统(Global Navigation Satellite System, GNSS)的逐步发展,其被广泛应用在军事、交通和农业等高精度定位服务领域。目前在轨的四大GNSS包括有中国的BDS,美国的GPS,欧洲的GALILEO以及俄罗斯的GLONASS,共计拥有导航卫星约125颗[60]。它们中的一些具备较好的兼容性和互操作性,将允许用户利用数据融合的方式同时使用多个星座进行组合导航,以满足自身较高的定位精度及可靠性要求。在使用卫星进行定位时,考虑到距离测算时所需的卫星钟和用户钟之间存在钟差,所以至少要使用四颗卫星才能完成位置解算。需要注意的是,信号从卫星内部生成并经过传输,最后到达用户接收机的整个过程中都存在各种影响测距的误差,而这些误差会导致定位精度受到损害,这就需要消除部分误差源或通过某些方式来削弱一些误差的影响。当测距误差一定时,接收机需在供选择的众多可见卫星中选择几何构型较好的卫星组合用于用户导航,以此将定位误差控制在可接受的范围内,这个过程被称为选星[61]。
目前学者们针对单、多星座导航的选星问题提出了各种方法,并多以几何精度因子(Geometric Dilution of Precision, GDOP)作为选星组合优劣的评判标准。除一些经典的选星方法[62]外,文献[63-65]中提出了一些基于卫星高度角和方位角的选星方法,在相应的星座系统下以较小的精度损失换来了选星效率的大幅提高;Wu等人[66]将统计学和机器学习方法用于选星,在GDOP值的逼近问题上测试了多种回归方法,结果表明支持向量机及遗传规划具备较好的性能;丁淑敏等人[67]将几何布局选星算法和准最佳选星算法结合,通过预设规则去除部分影响构型的卫星,以此减少所需遍历的卫星组合;
第6章 总结与展望
6.1 工作总结
智能优化算法的发展始于人们对某一自然现象或过程的观察,而后在实际生活中存在的优化问题上得到应用。因具备一些良好的特性而得到了众多学者的肯定,并带动一系列新型智能优化算法的提出,而天牛群优化算法便是其中的一个。该算法拥有易于实现,初始设定参数少等优点,吸引了许多学者对其进行研究。本文的主要工作则是对该算法进行改进研究并尝试将其应用于实际工程优化问题。
本文先是对智能优化算法的研究背景及意义进行了介绍,阐述了天牛群优化算法的发展过程以及国内外对该算法的研究现状,对论文的创新点进行了归纳,并给出了论文中每个章节的组织结构。
而后简单介绍了一些经典的智能优化算法,包括有遗传算法、粒子群优化算法以及烟花算法等。同时,文中详细解释了天牛群优化算法的基本原理、数学描述和伪代码。
对于天牛群优化算法存在的不足之处,文中给出了两种改进方式。一种是针对算法中起关键作用的速度更新公式进行改进,使用多个体联合决策的方式来处理其中的社会学习部分。另一种则是将Tent映射用于种群初始化,并在天牛位置更新步骤后加入云模型算子。前者有助于算法中的个体跳出局部极值,后者可以丰富算法的种群个体多样性。文中对改进策略的基本原理及算法的实现步骤都给出了较为详细的介绍,并在不同的测试函数集中进行了仿真实验,结果表明它们在不同程度上都增强了算法的寻优能力。
为探究天牛群优化算法在实际工程应用中的表现,文中在算法的个体位置表示上进行改进,提出了离散天牛群优化算法,并应用于卫星导航的选星问题。对于该组合优化问题的研究情况、数学描述以及算法在应用中的实现方式,文中同样给出了详细的描述,并在仿真环境中进行了一系列的测试,结果表明提出的选星方法具备一定的可行性。
参考文献(略)
