本文是一篇计算机论文范文,本文使用Java语言对算法进行了实现。我们先通过理论分析的方式对算法的优缺点和适用性进行了比较,然后通过不同的测试样例对本文所提出的两种算法与Wu在文献[70]所提出的全局算法相互进行比较,并验证了理论推导的正确性。
第一章 绪论
1.1 课题的研究背景与意义
现如今,计算机在社会生活中扮演的角色越来越重要,一旦计算机在运行过程中出现错误,将不可避免的带来或多或少的损失,尤其在各类故障敏感系统中,如交通运输、医疗等领域,计算机软、硬件系统的正确性和稳定性都显得尤为重要。软、硬件系统的可信度已经成为一个国家民生,政治经济和军事能否正常运转的关键之一[1]。为了可以更好地保证系统的正确性和稳定性,计算机科学工作者提出了形式化方法。
形式化方法是一种具有严格数学基础的软件及系统开发方法,用来对系统和软件进行分析、设计和验证,可以从根本上保障软件和系统的可靠性和安全性[2]。自形式化方法诞生以来,形式化方法一直受到计算机科学工作者的广泛关注。现在模型检测已经可以对状态数为20010的系统进行处理[3],同时一系列的验证工具,如NuSMV[4]、UPPAAL[5]、PAT[6]等工具的出现,使得形式化验证在实际中的应用得到了保证。在基于SMV[7]的验证中,IEEE Futurebus+896.1-1991在cache下的错误第一次被发现;美国电话电报公司(AT&T)在通讯软件的开发过程中,在7500条SDL代码的形式化验证中,找到了112个错误;空中防撞系统(TCAS)的使用形式规约语言RSML去刻画。形式化方法在各个领域发挥着越来越重要的作用。
采用形式化方法对进程间的等价关系进行自动验证一直备受计算机科学工作者的关注[8-11]。作为在众多的等价关系中非常重要的一个关系,互模拟可以用来识别具有相同行为的迁移系统[12,13],即满足互模拟关系的迁移系统可以互相模仿彼此的动作。互模拟是一种基于迁移系统的二元关系,具有严格的数学基础,可以良好的保持系统的性质。当两个迁移系统的初始状态满足互模拟关系时,可以称一个系统为另一个系统的抽象。互模拟被广泛的应用于计算机科学领域,尤其是在验证中,互模拟是状态聚合算法的基础[14]。互模拟可以将满足互模拟关系的状态使用一个抽象度较高的状态表示,从而减少系统验证的状态空间,有效地解决系统状态空间爆炸问题。
1.2 国内外研究现状
互模拟作为研究系统行为等价的重要概念,主要包括强互模拟,弱互模拟以及分支互模拟等。本文主要对强互模拟进行研究,并在下文中使用互模拟表示强互模拟。本节首先对传统互模拟的研究成果进行一些介绍,之后对基于概率的互模拟研究进行简要的回顾,最后对互模拟在模糊迁移系统下的研究现状进行说明。
1.2.1经典互模拟
对并发系统行为等价的研究一直是计算机科学界的热点,互模拟作为等价关系中最重要的概念之一,在过去的三十年中,受到了计算机科学工作者的广泛的关注并对其等价验证算法进行了深刻的研究。互模拟等价验证算法主要分为全局算法[25-27]和局部算法[28-30]两大类。
在全局算法中,算法需要对迁移系统的整个系统空间进行存储,在算法运行的过程中,始终需要知道整个迁移系统的迁移关系。全局算法建立在划分精华的思想基础上,即通过迁移关系及其后继状态对状态集合进行不断的划分,当无法继续划分时,所有满足互模拟关系的状态都在一个等价类集合中,此时,互模拟等价类划分完成。互模拟等价类划分完成之后,在对任意的状态是否满足互模拟关系进行判定时,不需要重新执行算法,只需要对状态对是否处于同一等价类中进行判断即可,具有较好的效率。
关于互模拟等价验证全局算法的研究已经持续了半个世纪。1965年,在对自动机的压缩问题进行研究时,Harrison和McCluskey第一次使用了全局算法的思想,该算法的时间复杂度为2|an|,其中a为动作的个数,n为状态的个数。Paige和Tarjan于1987年在文献[25]中利用划分精化的方法,在标签唯一的情况下,提出了不确定型迁移系统的互模拟等价类划分算法,该算法的时间复杂度为O(mlog n),其中n为状态的个数,m为迁移的个数。2004年,针对标签不唯一的情况,Pizza和Dovier等人提出将标签转换为新状态的方法[26],同时依据新状态所代表的标签进行划分,在该思想下,系统的等价类划分算法的时间复杂度降低到了O(mlog m)。
第二章 预备知识介绍
2.1 集合的划分与等价类
一般情况下,集合主要用于表示一些具有相同性质的东西汇集成的整体。在对集合的研究中,除去对两个不同集合进行研究外,对集合子集以及集合元素关系的研究也尤为重要。首先,我们对集合子集的性质进行一些简单的回顾。
1976年,迁移系统(Transition System, TS)由R. M. Keller提出,是一种描述计算机软硬件系统行为的抽象模型,也被用于对计算机软硬件系统的行为进行抽象建模。在使用迁移系统对计算机软硬件系统进行建模时,迁移系统中的每一个迁移都用来表示计算机软硬件系统中的一个原子操作。在迁移系统中,状态用于对系统的行为信息进行描述,迁移关系用于表示系统状态之间的转换,动作用于表示进程之间的通信行为和机制。若在系统的一系列迁移中,状态可以在动作下执行某一个迁移,则该系列迁移就是状态可行的迁移;若在每一个状态中选择一个迁移,将系统迁移至新的状态且存在可迁移的状态,那么该过程将不断的进行下去。
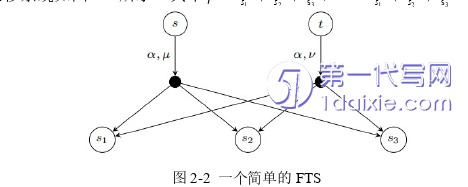
在迁移系统中,若一个状态在一个动作下只能到达一个状态,则称其为确定型迁移系统;若一个状态在一个动作下可以到达多个状态,即迁移到达哪一个状态的选择是非确定的,则称其为非确定型迁移系统。
2.2实现细节和时间复杂度分析
本小节采用面向对象的方法对算法3的数据结构进行详细说明。在算法3的实现过程中,我们采用邻接列表的方式对模糊迁移系统(FTS)进行存储。为了更好的对算法的实现进行描述,在面向对象方法的基础上,我们通过对类的描述来对数据结构进行说明。在实现该算法的过程中,主要对结点类Vertex,模糊迁移TPElements,状态划分块StateBlocks以及迁移划分块TPBlocks进行了实现。
结点类Vertex主要包含以下属性:
1.name:用于存储结点的标号;2.actionTrans:用于存储结点的迁移。
在结点类Vertex中,name可以为任意的数据类型,actionTrans使用HashTable来存储,主要对所有的模糊迁移进行存储,其中key值的数据类型与模糊迁移类TPElements中perAction的数据类型保持一致,value的值与模糊迁移类TPElements中disElement的数据类型保持一致。在获取图的结点时,使用构造器Vertex(name,actionTrans)对结点进行初始化。
模糊迁移类TPElements主要包含以下属性:
preStates:用于存储该模糊分布的前驱节点; 2.perAction:用于存储该模糊分布的前驱动作;第三章 模糊互模拟等价类划分算法 ............................... 15
3.1初始化算法 ...................................... 15
3.2 模糊互模拟等价类划分算法 .................................... 17
第四章 模糊互模拟等价验证的局部算法 .................................. 29
4.1 局部算法中的相关概念 ............................................ 29
4.2 模糊互模拟等价验证的局部算法 ........................... 31
第五章 算法的实现与比较分析 .......................... 39
5.1 算法的优缺点及适用性 ....................................... 39
5.2 算法的实现与对比 ...................................... 40
第五章 算法的实现与比较分析
5.1 算法的优缺点及适用性
本小节首先从理论上对模糊互模拟等价类划分算法Wu算法优缺点和适用性进行分析,然后对模糊互模拟等价验证的局部算法与Wu算法进行比较,最后对本文所提出的模糊互模拟等价类划分算法和模糊互模拟等价类验证的局部算法进行分析。
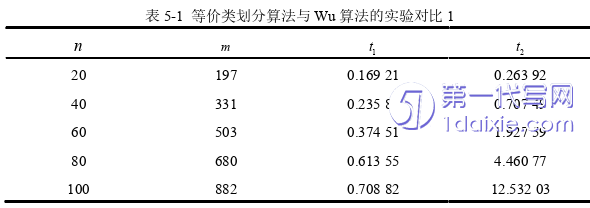
H. Y. Wu在文献[70]中所提出全局的时间复杂度为2 4O(m n),而本文所提出的模糊互模拟等价类划分算法的时间复杂度为O(mn(log mn))。两者都是全局算法,但是本文所提出算法的时间复杂度要明显优于Wu算法。
本文第三章所提出的模糊互模拟等价类划分算法与Wu算法都为全局算法,而第四章所提出的模糊互模拟等价验证算法为局部算法。从存储空间看,模糊互模拟等价验证的全局算法,由于在执行算法时,需要始终存储系统的全部状态,因此在执行算法的过程中,会浪费掉许多不必要的存储空间。从文章的第四章可知,第四章所提出的模糊互模拟验证的局部算法,只需要对要验证的状态及其后继状态进行遍历即可。 从算法的执行效率来看,全局算法对任意的两个状态是否满足模糊互模拟关系进行比较时,都需要求出所有的模糊互模拟等价类,或者说找出所有的满足互模拟等价关系的状态对。此时,在对其他任意两个状态对进行模糊互模拟等价关系判断时,只要对算法最后的运行结果进行遍历即可。当运行Wu算法时,若两个状态组成的状态对在最后的模糊互模拟等价关系集合中,则该状态对满足模糊互模拟等价关系。当运行本文所提出的模糊互模拟等价类划分算法时,若两个状态在同一个等价类中,则该状态对满足模糊互模拟关系。由于执行完模糊互模拟等价类划分算法后,所有满足模糊互模拟关系的状态都在同一个等价类中,故可以将同一个等价类中的状态用一个状态表示,从而实现状态聚合,有利于形成抽象程度更高的系统。
第六章 总结与展望
互模拟作为迁移系统中的经典概念,是模型检测的重要组成部分,主要用于形容系统间的行为等价性。互模拟是聚合算法的基础,是解决状态空间爆炸问题的主要手段。在经典的迁移系统中,对互模拟等价验证算法的研究已经取得了丰富的成果。在模糊领域,虽然对模糊互模拟的研究已经取得了丰硕的研究成果,但对模糊互模拟等价验证算法的研究却涉及不多。本文在已有模糊迁移系统和模糊互模拟定义的前提下,结合已有的互模拟等价验证技术,给出了模糊互模拟的等价类划分算法和模糊互模拟等价验证的局部算法。
首先给出了模糊互模拟的等价类划分算法,该算法是全局算法的一种,可对系统中满足模糊互模拟的状态进行等价类划分。同时,也可用于对图中的任意状态是否满足模糊互模拟关系进行判断。在给出模糊互模拟等价类划分算法之前,先依据动作对状态进行等价类划分,即将具有相同动作的状态划分到一个集合中并据此给出状态的划分算法。之后,利用迁移对状态进行划分,并据此提出关于状态划分的函数,与此同时,利用状态对迁移进行等价类划分,并在此基础上给出迁移划分的函数。然后,在以上函数的基础上,给出了模糊互模拟等价类划分算法。最后我们给出了实现该算法的具体数据结构和实现细节,并对算法的时间复杂度进行了分析,该算法的时间复杂度为O(mn(log mn)),其中n为模糊迁移系统的状态数目,m为模糊迁移的迁移数目。
接下来,给出模糊互模拟等价验证的局部算法。当只需要对给定状态对进行互模拟等价验证判断时,尤其在对两个不满足模糊互模拟关系的状态进行验证时,不必要对全部的状态进行遍历,局部算法拥有更好的效率。对此,提出了模糊互模拟等价验证的局部算法。局部算法结合已有的对提升关系进行判断的算法,一边对系统进行深度优先遍历,一边判断状态是否满足模糊互模拟关系。局部算法只需要对系统的部分空间状态进行遍历便可以对给定状态是否满足模糊互模拟等价关系进行判断。同时,我们给出了实现该算法的数据结构,并在此基础上分析该算法的时间复杂度。模糊互模拟等价验证的局部算法的时间复杂度为31 2 1 23O(m m nn),其中1n和2n分别为两个模糊迁移系统的状态数目,1m和2m分别为两个模糊迁移系统的迁移数目。
最后,我们使用Java语言对算法进行了实现。我们先通过理论分析的方式对算法的优缺点和适用性进行了比较,然后通过不同的测试样例对本文所提出的两种算法与Wu在文献[70]所提出的全局算法相互进行比较,并验证了理论推导的正确性。
参考文献(略)
