本文是一篇管理学论文,本文在一致性和共识性分析过程中,改进一致性和共识性完全通过构建模型。但选择直接将原偏好信息返回给决策专家进行修正,不仅时间成本高,而且也很难实现。因此可以将构建模型与主动反馈机制相结合,提出一种交互的一致性改进算法。
第一章绪论
第一节研究背景与意义
本节将从模糊集、犹豫模糊集、概率犹豫模糊集和区间概率犹豫模糊集的群决策过程,理顺偏好关系的发展脉络,从而概述本文的研究背景。同时,将从理论意义和实践意义两方面探讨本文的研究意义。
一研究背景
决策活动发生在人类日常生活中的各个方面,例如选择投资方案、制定营销方案、选择最优旅游地、供应商等。随着社会的发展,决策环境变得越来越复杂,充满了更多的不确定性,使得决策信息来源广、形式多样。在这种复杂环境下,决策问题很难由个人解决,且个人决策容易出现偏差。因此,需要多个决策专家共同参与,发挥群体的智慧来解决复杂环境下的决策问题。群决策作为一种可以集中群体优势和智慧的有效决策方法,已成为评价与决策研究领域的一个重要研究方向。
在群决策过程中,每位决策者需要对决策方案进行两两比较并给出相应的偏好值。Saaty[1]提出的层次分析法就是对某一准则下的各方案进行两两对比,利用1-9的精确数值来说明其重要程度,并按其重要性程度评定等级的一种决策方法。然而决策环境的不确定性导致决策者给出的偏好值不能以精确数形式表示,这种基于精确数的决策信息表达容易造成信息的缺失。于是Zadeh[2]提出的模糊集概念,用评价对象的隶属度表示其决策结果。Orlorski[3]和Tanino[4]通过模糊数来表示一个事物优于另一个事物的程度,提出并研究了模糊偏好关系。基于模糊偏好关系的群决策方法在收集和处理决策信息时,可以更好的刻画决策信息的模糊性,弥补了用精确数给出评价结果易造成信息缺失的问题。但当决策者面对复杂决策环境,经常会出现在几个评估值之间犹豫不决的情形,因此Torra[5]在模糊集概念的基础上提出了犹豫模糊集的概念,即每个犹豫模糊元是由若干个数值构成的集合。随后,Xia和Xu[6]提出了犹豫模糊偏好关系。基于犹豫模糊偏好关系的群决策方法在处理决策信息时从模糊性和犹豫性两个角度刻画决策者的不确定性程度,包含的决策信息更加全面。
第二节研究思路与内容
一研究思路
本文首先定义了区间概率犹豫模糊偏好关系,并从加性和乘性两个角度来解决偏好关系存在的不一致性问题。提出区间概率犹豫模糊偏好关系的加性一致性指数与乘性一致性指数,并构建模型改进一致性。其次考虑到存在区间概率犹豫模糊不完全偏好关系,本文基于一致性来构建模型补全缺失的偏好值。最后,将一致性分析与群体共识性分析相结合,构建加性一致的区间概率犹豫模糊偏好关系群决策模型和乘性一致的区间概率犹豫模糊偏好关系群决策模型。并将其应用至突发事件的网络舆情风险评估。
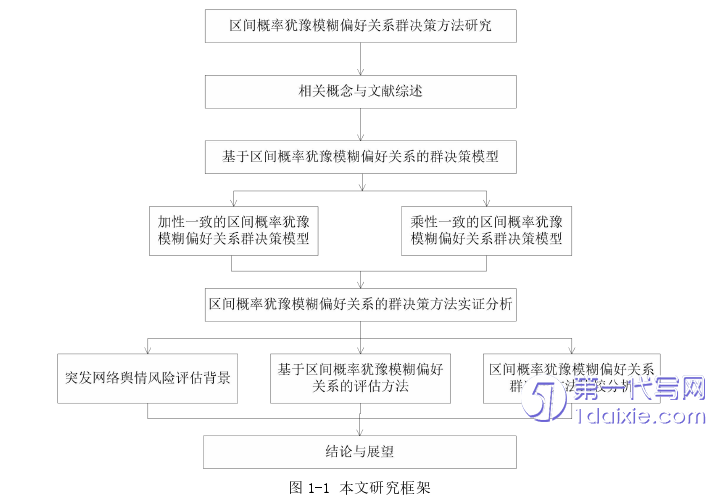
本文的研究框架如图1-1所示。
第二章相关概念与文献综述
第二节文献综述
本节梳理了模糊集和模糊偏好关系发展历程,介绍了各种模糊环境下的偏好关系和不完全偏好关系在一致性和共识性方面的研究现状,并分析了目前该领域研究现状存在的不足。
一区间概率犹豫模糊集
在决策信息表达方式的发展过程中,主要克服以下两个困难,一是专家主观层面上的模糊性和犹豫性,二是不同隶属度的重要程度不同。
其中模糊性是指专家在对目标进行评价时给出的模糊不清的一个范围。针对这一问题,Zadeh[2]提出的模糊集以及后续的拓展形式给出了较好解决方案,比如梯形模糊数,三角模糊数等。它们利用模糊数代替精确数来刻画初始评估值。Atanassov[13]提出了直觉模糊集的概念,它同时考虑隶属度、非隶属度和犹豫度,用犹豫度来描述非此非彼的模糊概念,更细腻的刻画客观世界的模糊性本质。而犹豫性则是指专家在对目标进行评价时,评估值会在几个可能的值之间犹豫不决,Torra[5]提出的犹豫模糊集很好的解决了这一问题,它允许专家在评价时将几个可能的值全部作为隶属度,即允许一个元素出现多个隶属度,但默认这些隶属度的重要性是相同的。
然而由于专家的主观性和数量等原因,不同隶属度应有不同程度的重要性。为克服此困难,Zhang[7]提出概率犹豫模糊集的概念。它为每个隶属度添加了一个相对应的概率,很好的表达了不同隶属度之间不同的重要程度。为进一步满足日益复杂的决策需求,增加决策信息表达的精确性与细致程度。Krishankumar[11]将隶属度对应的概率拓展为区间,提出区间概率犹豫模糊集。同时定义了简单的区间概率犹豫模糊加权几何平均算子,通过VIKOR方法应用该算子进行多属性决策。Song[12]基于区间概率犹豫模糊加权平均算子和区间概率犹豫模糊加权几何平均算子融合决策信息,提出可能度公式并构建可能度矩阵对方案进行排序。Krishankumar[14]又将Muirhead平均算子拓展到区间概率犹豫模糊集,对决策信息进行融合。
第二节加性一致的区间概率犹豫模糊偏好关系决策模型
本节主要研究区间概率犹豫模糊偏好关系的加性一致性以及基于加性一致性的群决策算法。首先提出基于区间概率犹豫模糊偏好关系的加性一致性定义、加性一致性指数和一致性改进模型,其次通过加性一致性分析构建模型补全区间概率犹豫模糊不完全偏好关系,最后提出适合区间概率犹豫模糊偏好关系和不完全偏好关系下加性一致的群决策算法。
通过梳理现有文献,在群决策过程中,决策者们给出若干偏好矩阵,刻画多个偏好矩阵的一致性程度用群体共识性指数来呈现,群体共识度指数主要集中于两种算法,一是文献[28]提出的通过融合所有偏好矩阵之间的距离来衡量共识性,二是文献[33]提出的,首先通过集合算子集成所有的偏好矩阵,得到综合的偏好矩阵,再通过测量每一个偏好矩阵和该综合偏好矩阵的距离来衡量群体共识性。本节将采用第二类方法来进行计算群体共识度。

第三章区间概率犹豫模糊偏好关系的群决策模型.............................18
第一节区间概率犹豫模糊偏好关系相关概念...........................18
一区间概率犹豫模糊完全偏好关系........................................18
二区间概率犹豫模糊不完全偏好关系........................19
第四章区间概率犹豫模糊偏好关系群决策方法实证分析...............41
第一节突发网络舆情风险评估背景....................................41
一突发网络舆情背景介绍.................................................41
二突发网络舆情风险评估指标体系.................................42
第五章结论与展望.................................63
第一节研究结论..............................................63
第二节研究展望................................64
第四章区间概率犹豫模糊偏好关系群决策方法实证分析
第一节突发网络舆情风险评估背景
本节主要介绍突发网络舆情风险评估的背景、突发网络舆情风险的主要评估指标以及群决策专家的偏好关系。
一突发网络舆情背景介绍
在一些社会事件突发后,往往会有一些虚假的信息和错误的观点迅速出现在各大网络平台,并演化为突发的网络舆情事件。例如,突发公共卫生事件、大型灾难事件与突发食品安全事件等都会在网络上引起热议,从而形成突发网络舆情事件。这些突发的网络舆情事件往往涉及多方利益、危害大,还会扰乱网络平台正常的运营秩序以及社会公共安全。因此针对突发网络舆情事件的风险评估就显得格外重要,及时、科学地对突发网络舆情事件进行风险评估,有利于在有限的资源内为风险程度更高的突发网络舆情事件提供有效的解决措施。
然而,目前网络平台众多,网络环境愈加复杂,导致决策者在进行突发网络舆情事件的风险评估时,需要面对大量的不确定性信息,主要有以下两个难点:一是难以直接给出评估值,二是无法以精确数的形式来表达决策信息。而区间概率犹豫模糊偏好关系是通过对事件两两比较从而获得某个评价指标下的偏好值,这可以克服决策者无法直接给出评估值的问题。同时,区间概率犹豫模糊偏好关系通过区间概率犹豫模糊元来表达偏好,可以全面准确的刻画决策者的偏好信息。因此,通过区间概率犹豫模糊偏好关系的群决策方法对突发网络舆情事件进行风险评估,不仅可以使得决策者的评估信息表达更全面,还保证了决策结果的合理性。

第五章结论与展望
第一节研究结论
本文对区间概率犹豫模糊偏好关系群决策问题展开了深入系统的研究,具体的研究成果如下:
(1)现有文献对区间概率犹豫模糊集刚展开研究,并未拓展偏好关系领域。本文提出了区间概率犹豫模糊偏好关系和相关的运算法则,以及区间概率犹豫模糊不完全偏好关系,并应用复杂环境下的群决策问题中,研究结果表明了该群决策模型充分考虑了偏好信息的全面性以及合理性,使得决策结果更符合实际。
(2)本文基于偏好关系的基本特性,首先定义了区间概率犹豫模糊偏好关系的的弱一致性,加性一致性,乘性一致性,然后提出了弱一致性的判定定理,加性一致性指数,乘性一致性指数,并结合群体共识性指数来构建模型改进决策专家给出的偏好矩阵,最后本文应用加性一致性分析和乘性一致性分析以及群体共识性分析,补全缺失的偏好关系并建立决策模型,将其应用到区间概率犹豫模糊偏好关系的多属性群决策问题中,研究结果表明了该决策模型多属性群决策问题中考虑到存在不完全偏好信息,更加符合实际决策环境。
(3)考虑到目前概率犹豫模糊偏好关系的一致性指数只是从距离方面来衡量偏好矩阵的一致性,本文在定义一致性指数和群体共识性指数时,加入秩相关系数,从而可保证从距离和顺序两个维度来衡量一致性和共识性。另外在现有文献中,偏好关系的群决策问题并未考虑到各备选方案的多个属性,而直接给出综合偏好矩阵,本文选出备选方案的常用评价指标,决策专家需要在每个评价指标下给出偏好矩阵,研究结果表明该决策结果获得了更加合理的决策结果,更加符合复杂的决策环境。
参考文献(略)
